1.4.4 Liczby kwantowe
Rozwiązaniem równania Schrödingera są pewne funkcje własne, które można scharakteryzować przy pomocy zestawu trzech liczb kwantowych n, l, m. Liczby kwantowe nie mogą być dowolne, muszą przyjmować jedynie pewne wartości. Liczba n jest nazywana główną liczbą kwantową może przyjmować wartości kolejnych liczb naturalnych (całkowitych, dodatnich): 1, 2, 3...... Poboczna liczba kwantowa l może przybierać wartości 0, 1, 2... (n - 1). Liczba m nazywana jest magnetyczną liczba kwantową. Liczba m osiąga wartości z przedziału <-l,+l>. Zestaw tych trzech liczb kwantowych nosi nazwę orbitalu. Poszczególne orbitale określa się skrótami podanymi w tabeli 2, które zawierają głowną liczbę kwantową oraz poboczną liczbę kwantową, przy czym ta ostatnia podana jest w postaci litery. Przyjęto nazywać wartość l = 0 literą s, l =1 literą p, l = 2 literą d oraz l = 3 literą f. Litery te pochodzą od angielskich słów sharp, principle, diffuse, fundamental i zostały wzięte z określeń stosowanych dla określenia widm w analizie spektralnej.
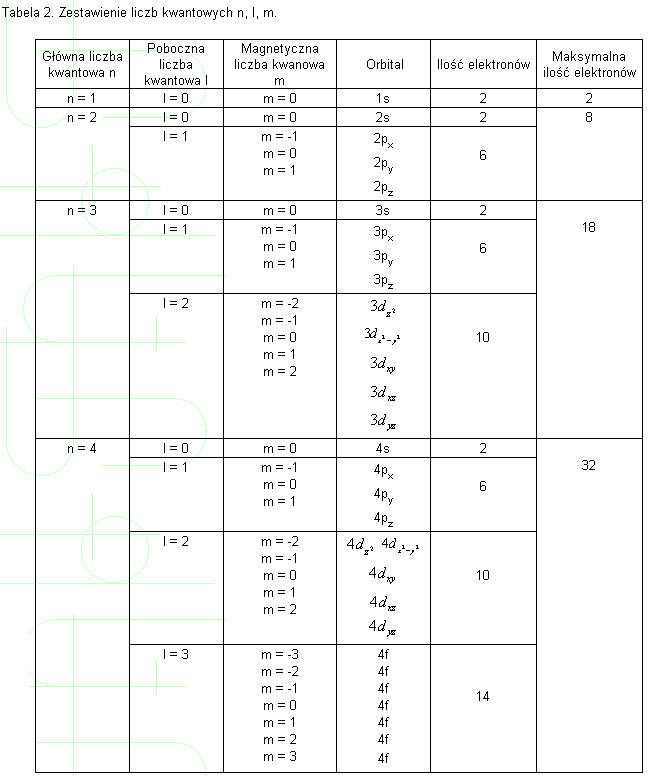
W tabeli 2 zestawiono wartości poszczególnych zestawów liczb kwantowych.