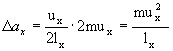2.1.1.2   Ciśnienie gazu

Rys.2.02 przedstawia rozkład prędkości na trzy składowe kierunkowe w układzie kartezjańskim x,y,z dla cząsteczki gazu o masie m poruszającą się  w jednostce objętości ograniczonej ścianami naczynia. Jeżeli cząstka taka ulegnie sprężystemu odbiciu z prostopadłą do kierunku x ścianą nastąpi zmiana zwrotu prędkości i średni pęd cząsteczki po odbiciu wyniesie .

Rys.2.02. Rozkład składowych prędkości cząsteczki poruszającej się w jednostce objętości.

Zmiana pędu wywołana zderzeniem jest więc równa:

Równanie (2.01)                   

Jeżeli długość naczynia w kierunku x wynosi to czas upływający między kolejnymi zderzeniami cząsteczki z ta samą ścianą wyniesie            a częstość zderzeń będzie jego odwrotnością: .

Sumaryczna zmiana pędu w jednostce czasu  będzie równa iloczynowi częstości zderzeń i zmiany pędu odpowiadającej pojedynczemu zderzeniu:

Równanie(2.02)                  

Ściana działa na każdą cząstkę siłą F, której bezwzględna wartość jest równa zmianie pędu:

Równanie(2.03)                  

Siła ta odniesiona do i cząstek uderzających o jednostkę powierzchni ściany jest miarą wywieranego przez gaz ciśnienia na ścianę naczynia:

Równanie(2.04)                  

Wykorzystując geometryczny związek pomiędzy średnią prędkością wypadkową u a jej składowymi kierunkowymi  względem trzech osi:

Równanie (2.05)                 

oraz zależność:

Równanie (2.06)                 

mamy:

Równanie (2.07)                 

gdzie u² jest średnim kwadratem prędkości niezależnym od kierunku ruchu.

Podstawiając (2.07) do (2.04 ) otrzymamy:

Równanie (2.08)                 

Ponieważ iloczyn    jest objętością naczynia V mamy:

Równanie (2.09)                 

Równanie (2.9) wyprowadzone dla gazu doskonałego jest podstawowym równaniem wiążącym ciśnienie gazu p ze stężeniem cząsteczek wyrażonym przez   oraz ze średnim kwadratem ich szybkości . Równanie to można przedstawić w formie iloczynu ciśnienia i objętości:

Równanie (2.10)                 

Wprowadzając do wyrażenia (2.10) liczbę Avogadra (II.2.1.2.1)  uzyskujemy wartość  dla n moli gazu:

               (2.11)                 

gdzie a masa molowa gazu M (V.1.3.1) jest równa iloczynowi .