1.3.1 Pojęcia podstawowe
Jak zaznaczono to w rozdziale o budowie materii, masy atomów wyrażane są w jednostkach mas atomowych u. Wartość u wyrażona w gramach wynosi 1,660*10-24. Masy atomowe podane są w układzie okresowym przy symbolu pierwiastka. Suma mas atomów wchodzących w skład cząsteczki określa masę cząsteczki wyrażoną w jednostkach u. Nawet dla bardzo dużych cząsteczek, takich jak cząsteczki polimerów, masy są bardzo małe. Ze względów praktycznych, w obliczeniach i pracach laboratoryjnych posługujemy się inną, znacznie większą miarą ilości (liczności) materii. Stanowi ją mol. Jeden mol materii zawiera liczbę Avogadra równą 6,022*1023 składników. Jeden mol atomów zawiera, zatem liczbę Avogadra atomów. Jeden mol cząsteczek zawiera 6,022*1023 cząsteczek. Oznacza to, że 1 mol atomów wodoru zawiera 6,022*1023 atomów wodoru, 1 mol cząsteczek chloru zawiera 6,022*1023 cząsteczek Cl2, na 1 mol żelaza składa się 6,022*1023 atomów żelaza; tyle samo elektronów wchodzi w skład 1 mola elektronów. Bardzo ważną właściwością mola jest to, że masa 1 mola pierwiastka lub związku chemicznego, czyli masą molowa wyrażona w gramach, jest równa liczbowo masie atomu tego pierwiastka lub cząsteczki związku chemicznego wyrażonej w jednostkach mas atomowych u. Np. masa atomu wodoru wynosi 1 u, czyli 1,660*10-24 g. Masa molowa wodoru, czyli masa 1 mola atomów wodoru wynosi 1u*6,022*1023 mol-1, co oznacza 1,660*10-24 g*6,022*1023 mol-1 czyli 1 g/mol. A więc masa atomowa wodoru wynosi 1 u, a masa molowa wodoru 1 g/mol. Analogicznie masa atomu węgla wynosi 12 u, a masa molowa węgla 12 g/mol. Podobnie ma się z masami cząsteczek. Masa cząsteczki wodoru to 2 u, a masa molowa to 2 g/mol. W przypadku metanu CH4 masa cząsteczki wynosi 16 u, a masa molowa 16 g/mol.
Masy molowe pierwiastków podane są w układzie okresowym. Są to średnie masy charakteryzujące skład izotopowy pierwiastków w przyrodzie. Na przykład po uwzględnieniu składu izotopowego wodoru masa molowa wodoru wynosi 1,008 g/mol, a masa chloru 35,45 g/mol.
Przykład 4.
Oblicz ilość cząsteczek w 1,000 g metanu.
Rozwiązanie.
W
1 molu każdego związku znajduje się liczba Avogadra cząsteczek, NA =
6,022 * 1023 mol-1
Masa
molowa metanu
![]() . Zatem 1,000 g stanowi
. Zatem 1,000 g stanowi
![]() mola metanu. Z proporcji
mola metanu. Z proporcji
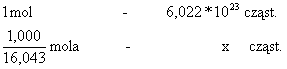
można wyliczyć x = 3,754*1022 cząsteczek.
Odpowiedź
W 1,000 gramie metanu znajduje się 3,754*1022 cząsteczek.
Wiele substancji występuje w stanie gazowym. Jest zrozumiałe, że substancje gazowe łatwiej charakteryzować podając ich objętość oraz warunki, w jakich nastąpił pomiar objętości. W rozważaniach dotyczących stanu gazowego użyteczne jest pojęcie gazu doskonałego. Ten wyidealizowany stan materii charakteryzuje się następującymi cechami:
a) cząsteczki będące punktami materialnymi o zaniedbywalnych wymiarach poruszają się ruchem postępowym po liniach prostych,
b) cząsteczki poruszają się chaotycznie, zderzając się ze sobą lub ze ściankami naczynia w sposób doskonale sprężysty,
c) cząsteczki nie oddziaływują na siebie do momentu zderzenia.
Gaz spełniający te założenia zachowuje się zgodnie z prawami gazów doskonałych (II.2.1.1.1):
a) prawem Boyle’a (przemiana izotermiczna): W stałej temperaturze objętość gazu jest odwrotnie proporcjonalna do ciśnienia, co można zapisać w postaci równania pV = const,
b)
prawem Gay-Lussaca (przemiana izobaryczna): Przy stałym ciśnieniu
objętość gazu jest odwrotnie proporcjonalna do temperatury,
![]() ,
,
c)
prawo Charlesa (przemiana izochoryczna): Przy stałej objętości
ciśnienie gazu jest odwrotnie proporcjonalne do jego temperatury,
![]() .
.
Uogólnieniem wyżej przedstawionych praw gazowych jest równanie stanu gazu:
![]()
Objętość
1 mola gazu doskonałego w warunkach normalnych (p = 101325 Pa, T = 273 K)
nosi nazwę objętości molowej i wynosi 22,414 dm3.
Podstawiając objętość
molową oraz parametry charakterystyczne dla warunków normalnych można
wyliczyć wartość wyrażenia
![]() . Wartość ta obliczona dla 1 mola wynosi
. Wartość ta obliczona dla 1 mola wynosi
![]() , jest oznaczana literą R i nosi
nazwę uniwersalnej stałej gazowej. Przekształcając odpowiednio równanie
stanu gazu i wprowadzając liczbę moli n, można otrzymać równanie
Clapeyrona (II.2.1.2.5):
, jest oznaczana literą R i nosi
nazwę uniwersalnej stałej gazowej. Przekształcając odpowiednio równanie
stanu gazu i wprowadzając liczbę moli n, można otrzymać równanie
Clapeyrona (II.2.1.2.5):
![]()
Przykład 5.
Oblicz ilość cząsteczek metanu zawartych w objętości v = 1,0 cm3 zmierzonej w warunkach normalnych.
Rozwiązanie
W 1
molu każdego związku znajduje się liczba Avogadra cząsteczek, NA =
6,022 * 1023 mol-1
Traktując
metan jako gaz doskonały można przyjąć objętość molową metanu 22,414
dm3. Objętość metanu v = 1,0 cm3 zmierzona w
warunkach normalnych stanowi
![]() mola metanu. Z proporcji
mola metanu. Z proporcji

można wyliczyć x = 2,7*1019 cząsteczek.
Odpowiedź.
W 1,0 cm3 metanu zmierzonym w warunkach normalnych znajduje się 2,7*1019 cząsteczek.
Przykład 6.
Oblicz objętość gazu doskonałego zawierającego 2,0*1020 cząsteczek w temperaturze 27 C pod ciśnieniem 100650 Pa.
Rozwiązanie
W 1 molu każdego związku
znajduje się liczba Avogadra cząsteczek, NA = 6,022 * 1023
mol-1
Znając ilość cząsteczek można wyliczyć ilość moli gazu:

Ilość moli gazu wynosi 3,3*10-4 mola. Objętość można wyliczyć z prawa Clapeyrona
![]()
Odpowiedź.
Objętość gazu w podanych warunkach wynosi 8,2 cm3.
Zapamiętaj!
We
wzorze Clapeyrona stała gazowa R
wyrażona jest w J/mol*K,
objętość
V w m3, przy czym
1
m3 = 1000 dm3
1
dm3 = 1000 cm3
1
l = 1 dm3
1
ml = 1 cm3
ciśnienie
w paskalach (Pa = N/m2)
Stosowane
są wielokrotności Pa
1
hPa = 100 Pa,
1
kPa = 1000 Pa,
1
MPa = 106 Pa
temperatura
T w skali Kelvina
(T
= t + 273,15).
t – temperatura w skali Celsiusza.
Przykład 7.
Oblicz ilość cząsteczek w 1,00 cm3 (war. norm.) trzech substancji: wodoru, wody oraz żelaza, znając gęstość żelaza d = 7,87 g*cm-3 oraz wody d = 1,00 g*cm-3.
Rozwiązanie
W 1 molu wodoru, wody oraz żelaza znajduje się liczba Avogadra cząsteczek lub atomów, NA = 6,022 * 1023 mol-1.
Liczbę cząsteczek zawartych w 1,00 cm3 (war. norm.) wodoru można wyliczyć z proporcji:

x = 2,7 * 1019 cząsteczek
Masa
1,00 cm3 wody obliczona ze wzoru m = d*V = 1.0 g, co odpowiada
![]() mola. Ilość cząsteczek można wyliczyć z proporcji:
mola. Ilość cząsteczek można wyliczyć z proporcji:

x = 3,3*1022 cząsteczek
Masa
1,00 cm3 żelaza obliczona ze wzoru m = d*V = 7,87 g, co
odpowiada
![]() mola. Zatem
mola. Zatem

x = 8,5*1022 cząsteczek
Odpowiedź.
Ilość cząsteczek lub atomów w 1 cm3 wodoru, wody i żelaza wynosi odpowiednio: 2,7 * 1019, 3,3*1022, 8,5*1022 cząsteczek.