Kształt cząsteczek
| Site: | Open AGH - Otwarte Zasoby Edukacyjne |
| Course: | Elementy chemii nieorganicznej dla geologów |
| Book: | Kształt cząsteczek |
| Printed by: | Gość |
| Date: | Tuesday, 16 December 2025, 9:12 AM |
1. Teoria VSEPR
VSEPR (Valence Shell Electron Pair Repulsion) - odpychanie par elektronowych powłoki walencyjnej
W metodzie VSEPR zakłada się, że spośród czterech rodzajów walencyjnych par elektronowych drobiny czyli par σ, par π, wolnych par atomu centralnego i wolnych par ligandów, tylko dwa rodzaje decydują o geometrii cząsteczki. Są to: wolne pary elektronowe atomu centralnego i pary σ łączące atom centralny z ligandami.
Podstawowym parametrem obliczeniowym metody VSEPR pozwalającym wyznaczyć kształt cząsteczki jest liczbą przestrzenną, Lp, którą stanowi łączna liczba wolnych par elektronowych atomu centralnego i par σ. Pary π nie wpływają na wartość liczby przestrzennej.
Metoda VSEPR ma swoje reguły i ograniczenia, które omówimy w kolejnych podrozdziałach.
 Nurtuje Cię pytanie Co oznacza skrótowiec VSEPR?*. Obejrzyj film, może uzyskasz odpowiedź.
Nurtuje Cię pytanie Co oznacza skrótowiec VSEPR?*. Obejrzyj film, może uzyskasz odpowiedź.
Film: Co oznacza skrótowiec VSEPR?*. Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.
_________________
* wykorzystano grafiki zamieszczone na Zintegrowanej Platformie Edukacyjnej.
1.1. Ograniczenia metody VSEPR
- Metoda może być stosowana dla drobin zawierających wyłącznie pierwiastki grup głównych.
- Drobina zawiera jeden atom centralny, definiowany jako atom otoczony innymi atomami lub grupami atomów i nie posiadający odpowiednika strukturalnego w danej cząsteczce, np. atom tlenu w cząsteczce wody; atom siarki w cząsteczce kwasu siarkowego(VI).
- Ligandy mogą stanowić jedynie pojedyncze atomy, a nie grupy atomów. W przypadku grup atomów stosuje się metodę liganda zastępczego. Ligand zastępczy to odpowiednio dobrany atom zastępujący grupę atomów w cząsteczce, a pozwalający na przedstawienie cząsteczki w postaci wzoru EAnHm i likwidujący ograniczenia w określeniu jej stereostruktury.
1.2. Reguły metody VSEPR
- Geometrię drobiny można przewidywać, dla struktur pozwalających się opisać w postaci EAnHm, gdzie E – atom centralny, A – atomy pierwiastków grup głównych, jednakowe lub różne, z wyjątkiem wodoru, H – atomy wodoru, n – łączna liczba ligandów typu A, m – liczba atomów wodoru.
- O przestrzennym rozmieszczeniu ligandów wokół atomu centralnego decyduje liczba przestrzenna (Lp), którą stanowi łączna liczba wolnych par elektronowych atomu centralnego (LwpE) i par σ.
- Orientacja
przestrzenna kierunków osi przestrzeni orbitalnych par elektronowych decydujących o budowie
przestrzennej drobiny jest maksymalnie symetryczna i zależy tylko od ich
liczby.
Liczba przestrzenna jednoznacznie określa orientację przestrzenną i może przybierać wartości 2, 3, 4, 5, 6, 7 i rzadko wyższe. - Wzajemne odpychanie się par elektronowych jest zgodne z zasadą: najsilniej odpychają się dwie pary elektronowe, słabiej odpycha się wolna para z parą σ, a najsłabiej dwie pary σ.
- Dla atomów stanowiących ligandy, musi być spełniona reguła helowca: dublet dla wodoru, oktet dla pozostałych pierwiastków.
1.3. Wartość liczby przestrzennej a struktury przestrzenne drobin
Liczba przestrzenna 2, symetria kierunków orbitalnych liniowa (diagonalna), LwpE = 0
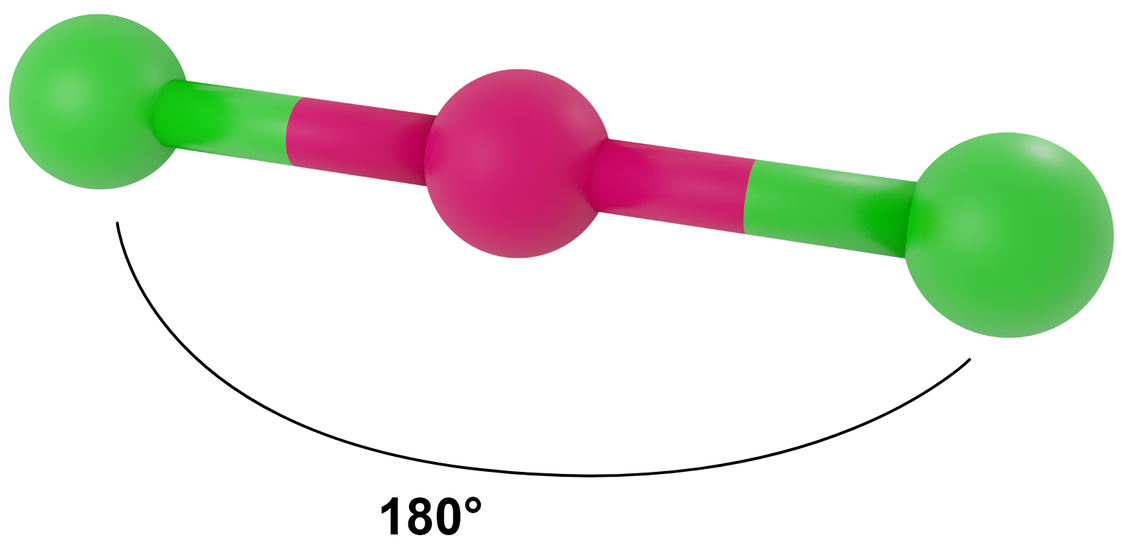
Przykłady: BeCl2, CO2
Liczba przestrzenna 3, symetria kierunków orbitalnych trygonalna
- dla LwpE = 0 - trójkąt równoboczny
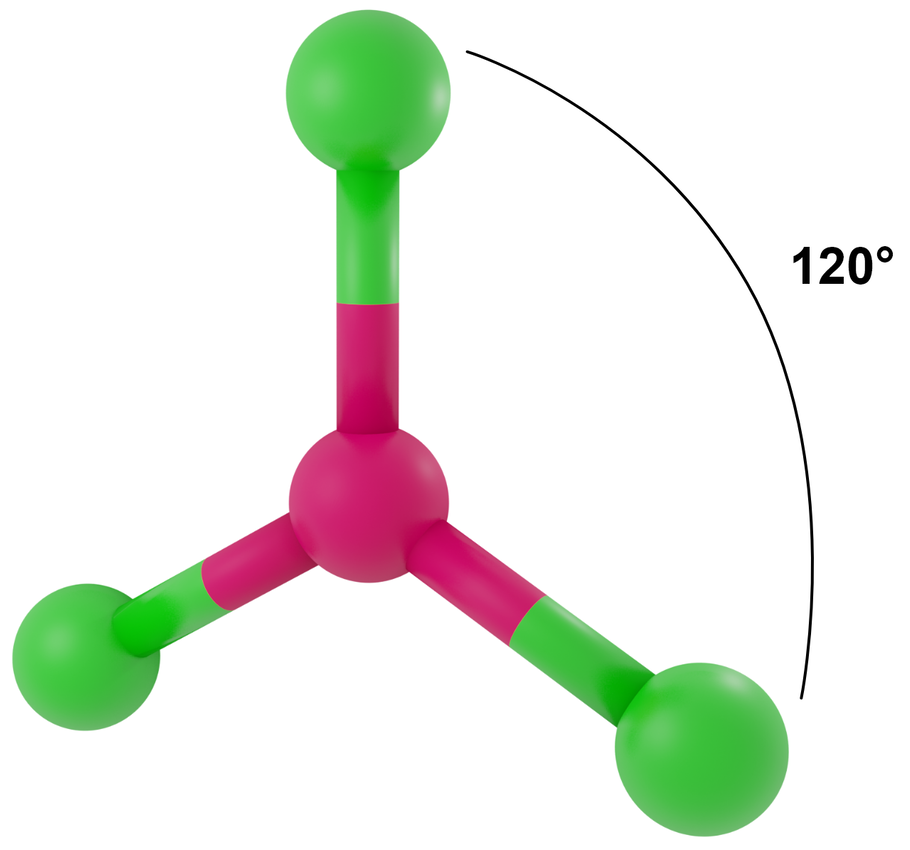
Przykłady: BF3, CO32-, NO3-, SO3
- dla LwpE = 1 - trójkąt równoramienny
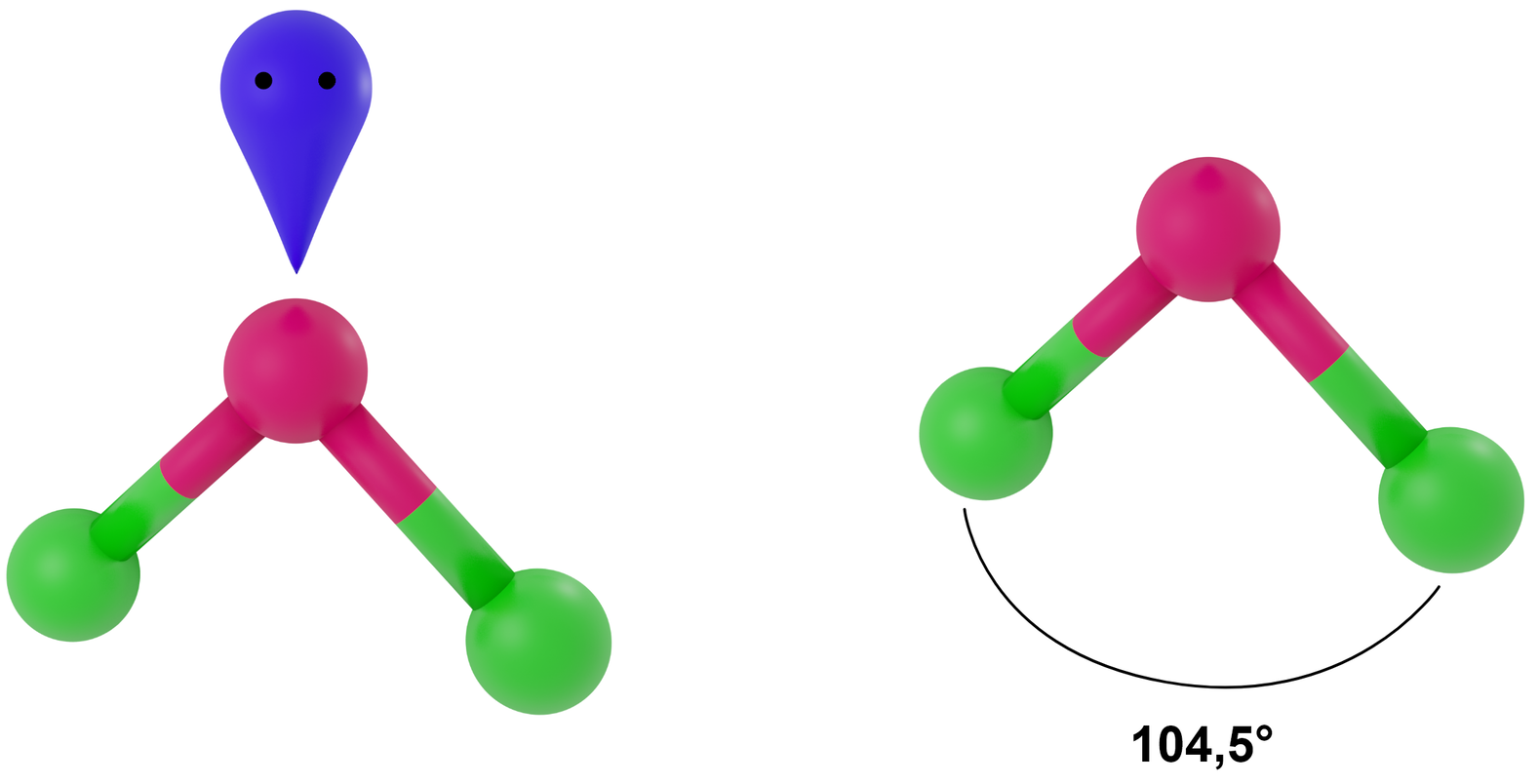
Przykłady: NO2-, SO2, O3
Liczba przestrzenna 4, symetria kierunków orbitalnych tetraedryczna
- dla LwpE = 0 - tetraedr
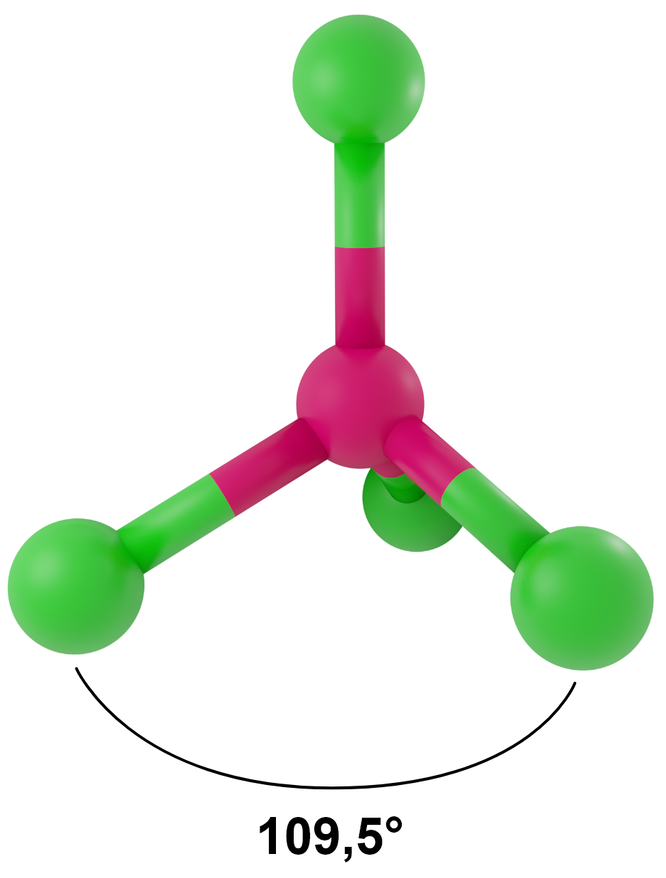
Przykłady: CH4, PO43-, SO42-, ClO4-
- dla LwpE = 1 - piramida trygonalna
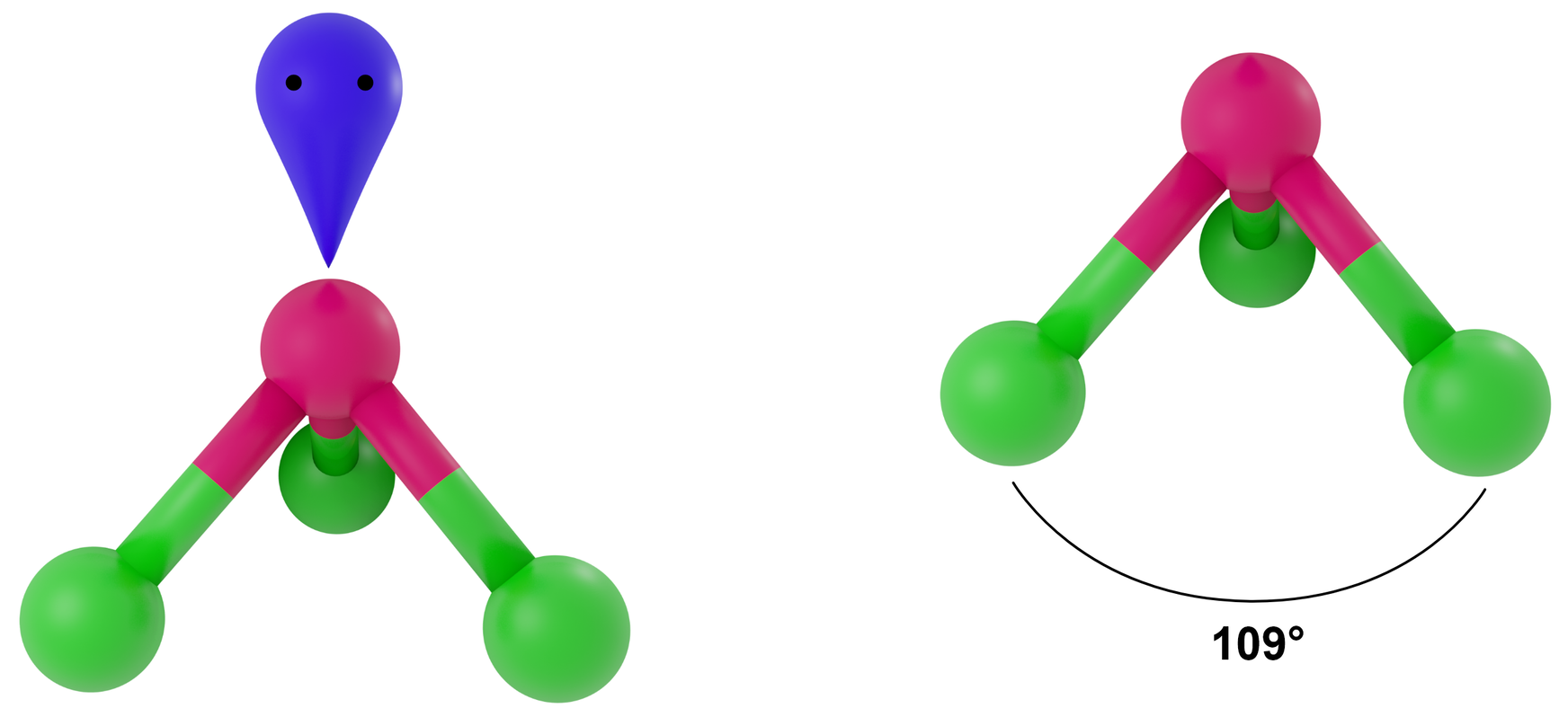
Przykłady: NH3, PCl3
- dla LwpE = 2 - trójkąt równoramienny
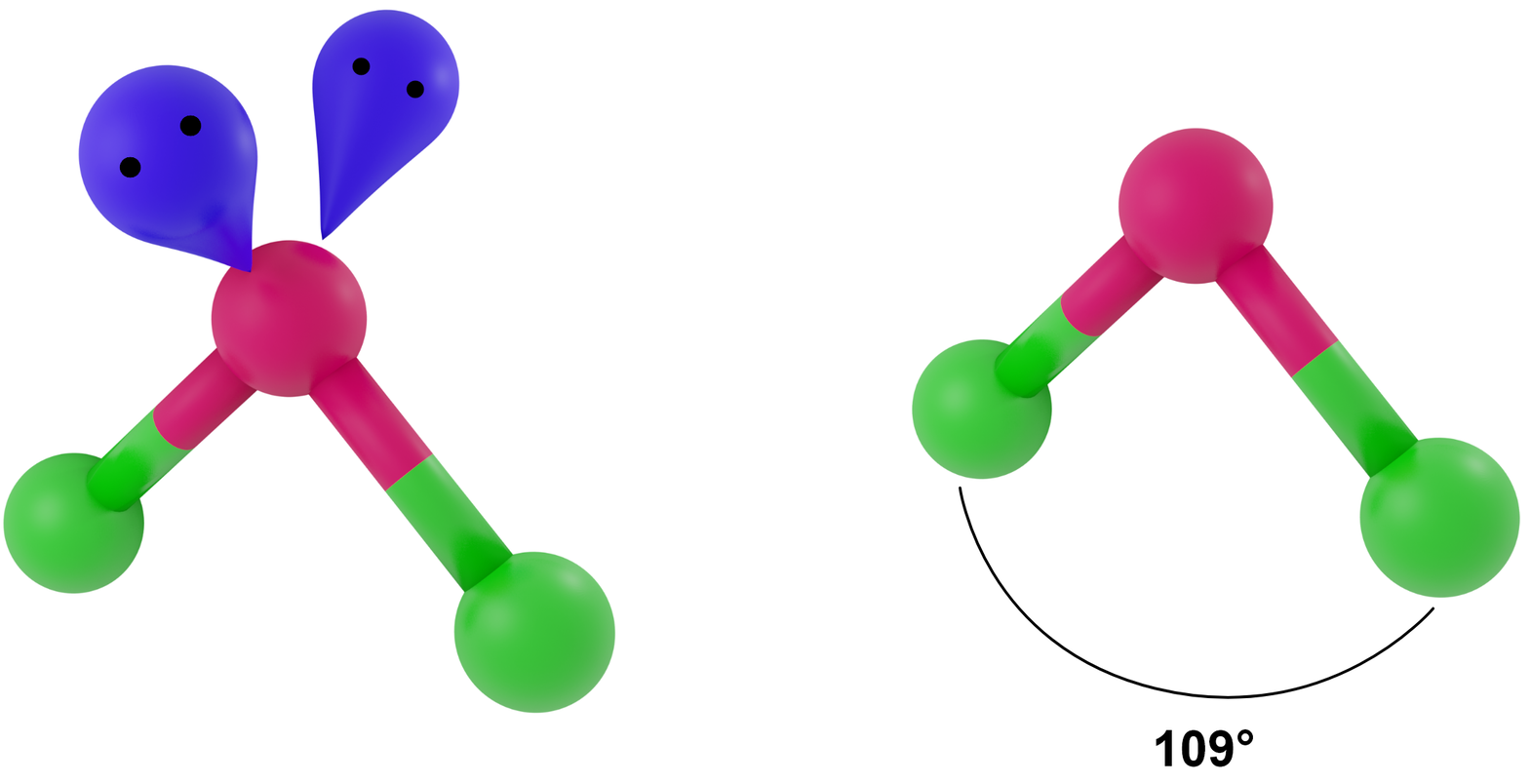
Przykłady: H2O, OF2
Liczba przestrzenna 5, symetria kierunków orbitalnych bipiramidy trygonalnej
- dla LwpE = 0 - bipiramida trygonalna
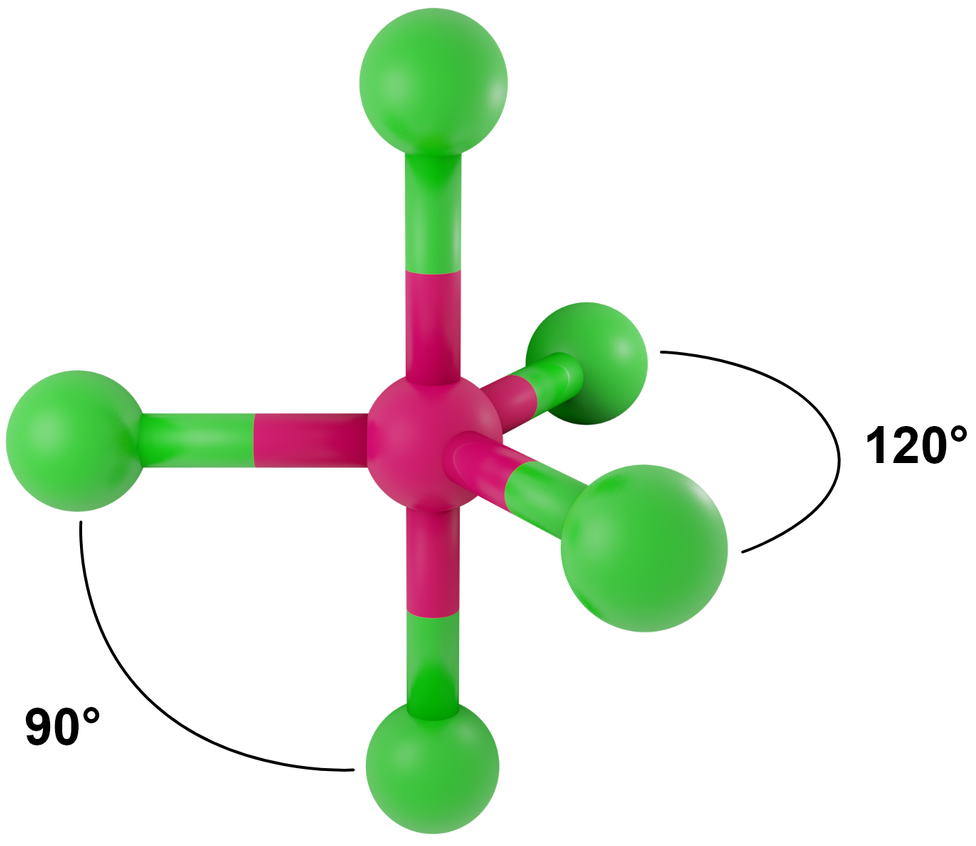
Przykłady: PCl5
- dla LwpE = 1 - zdeformowany tetraedr

Przykłady: SF4
- dla LwpE = 2 - deltoid wypukły
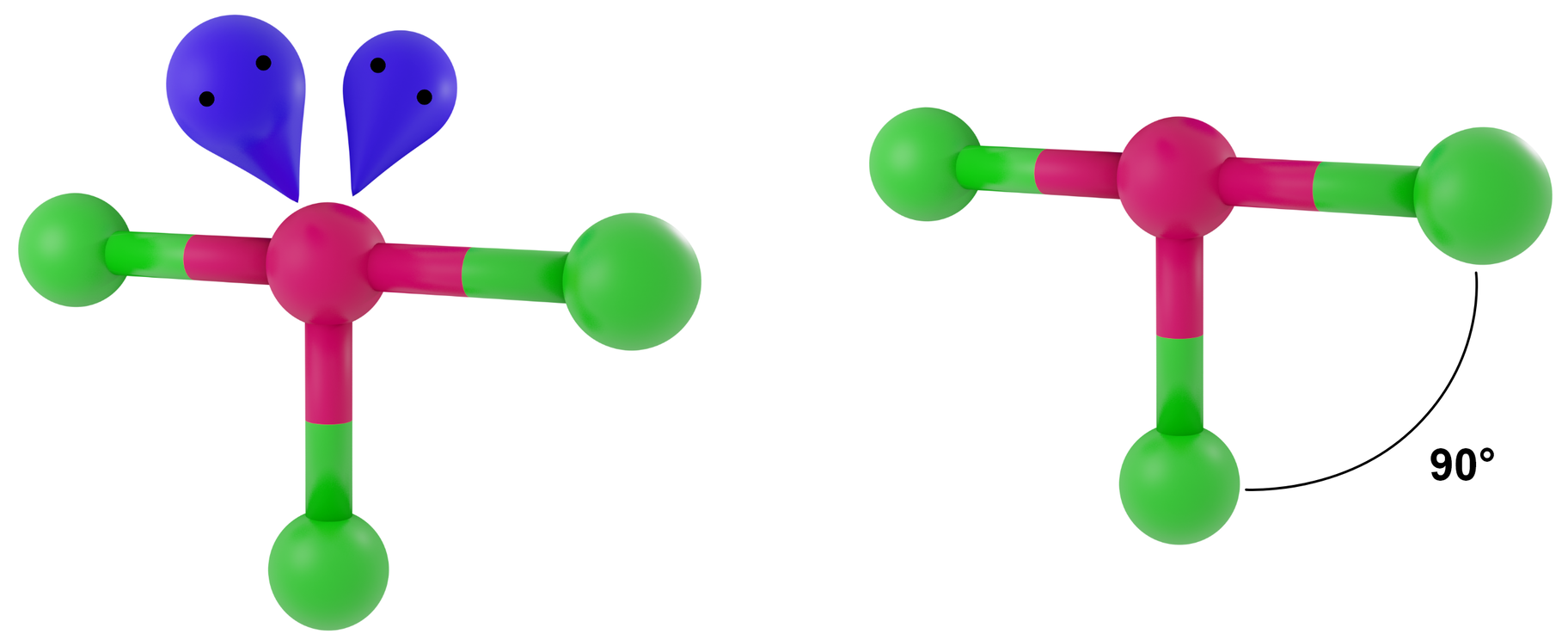
Przykłady: ClF3, BrF3
- dla LwpE = 3 - liniowa
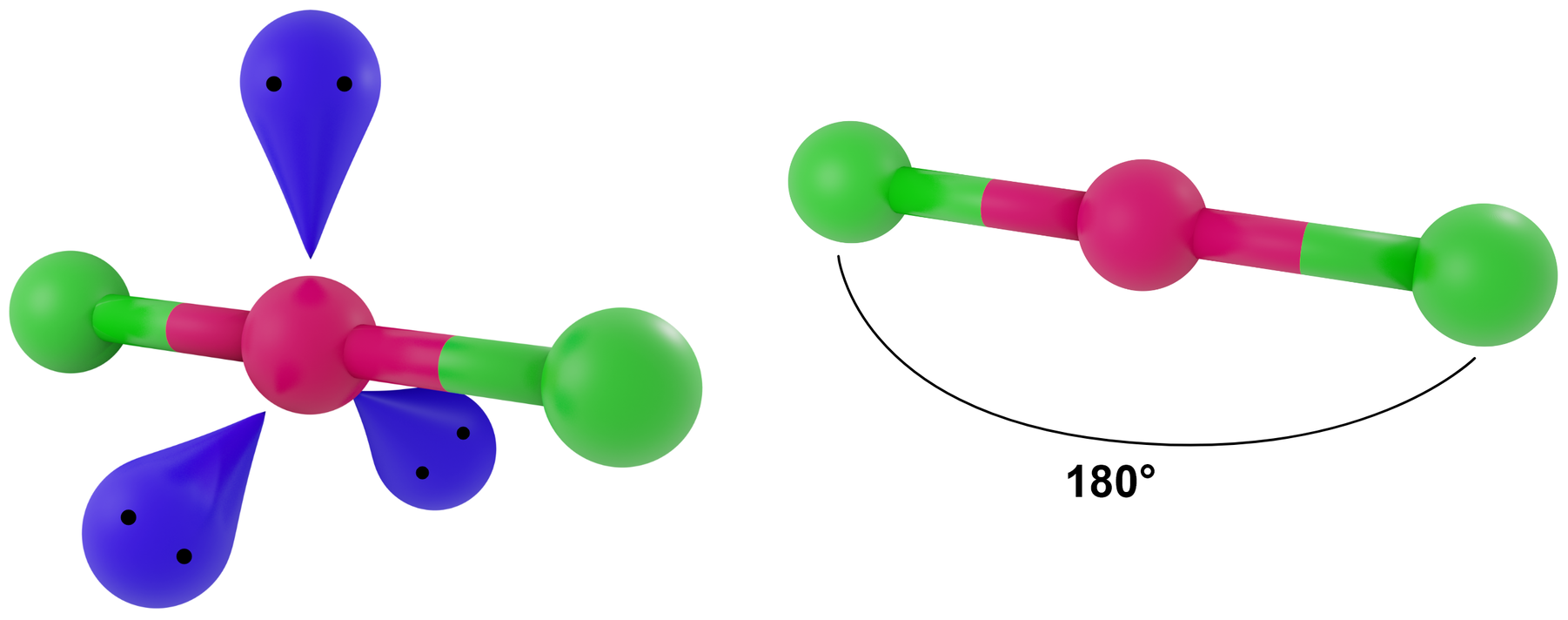
Przykłady: XeF2, ICl2-
Liczba przestrzenna 6, symetria kierunków orbitalnych bipiramidy tetragonalnej (oktaedru)
- dla LwpE = 0 - bipiramida tetragonalna (oktaedr)
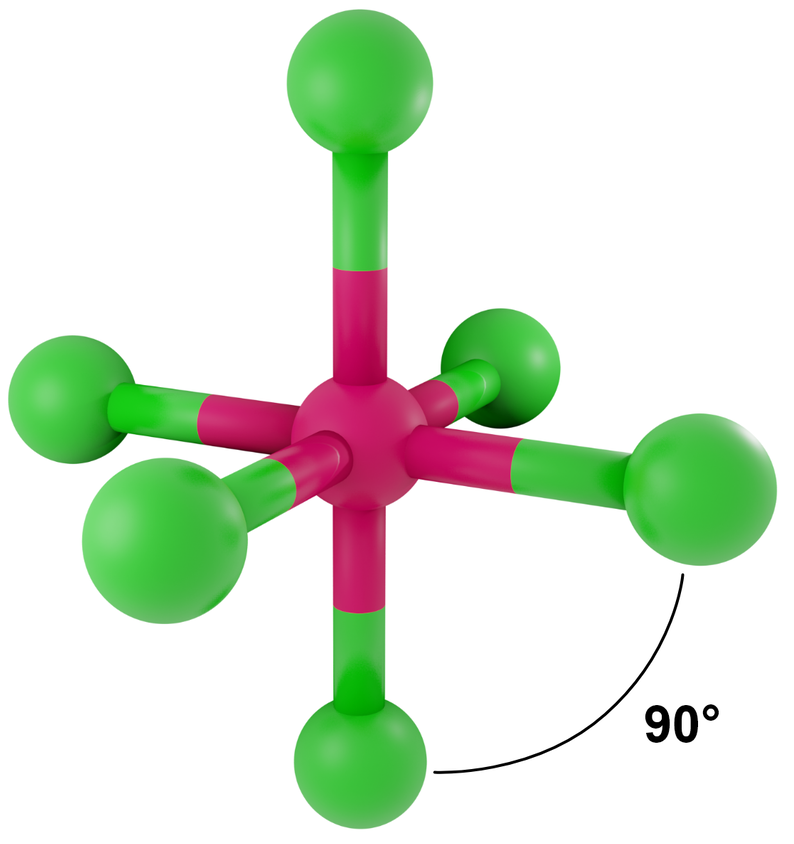
Przykłady: SF6
- dla LwpE = 1 - piramida tetragonalna
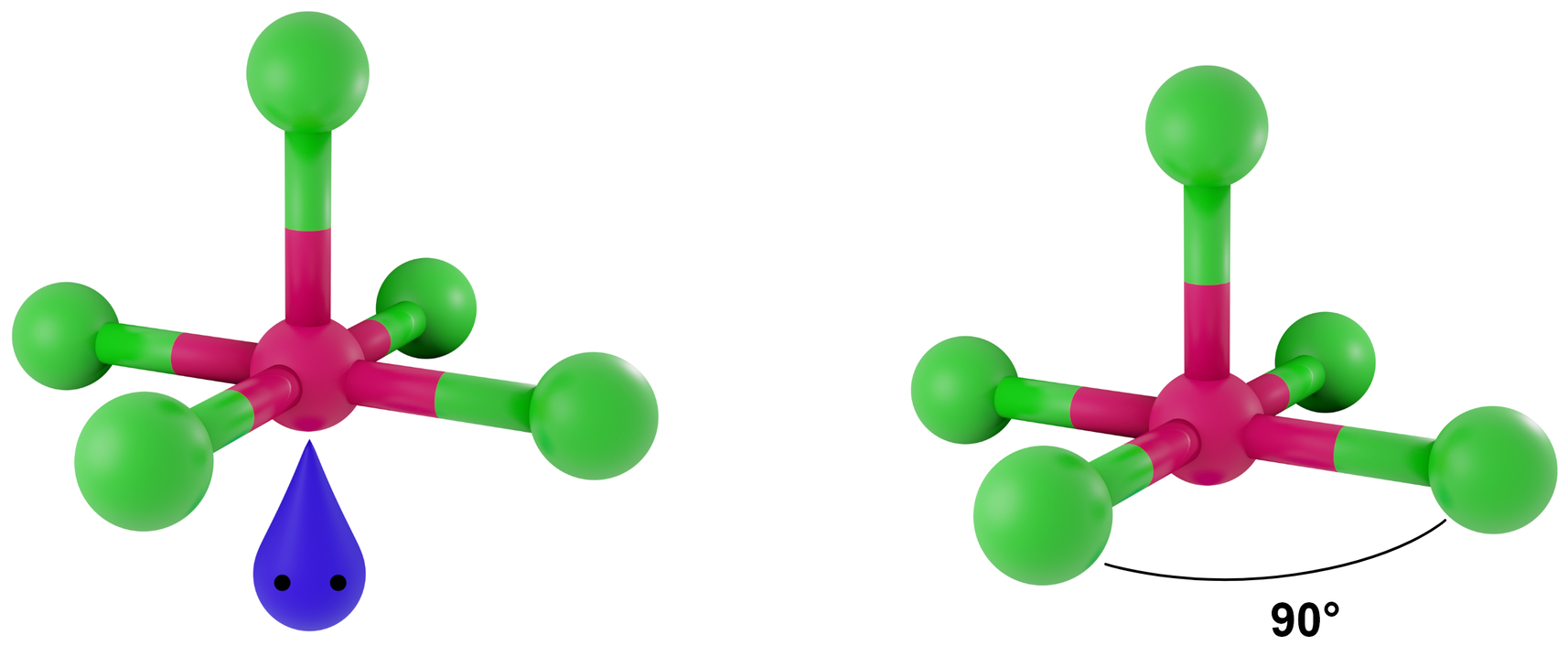
Przykłady: IF5
- dla LwpE = 2 - kwadrat
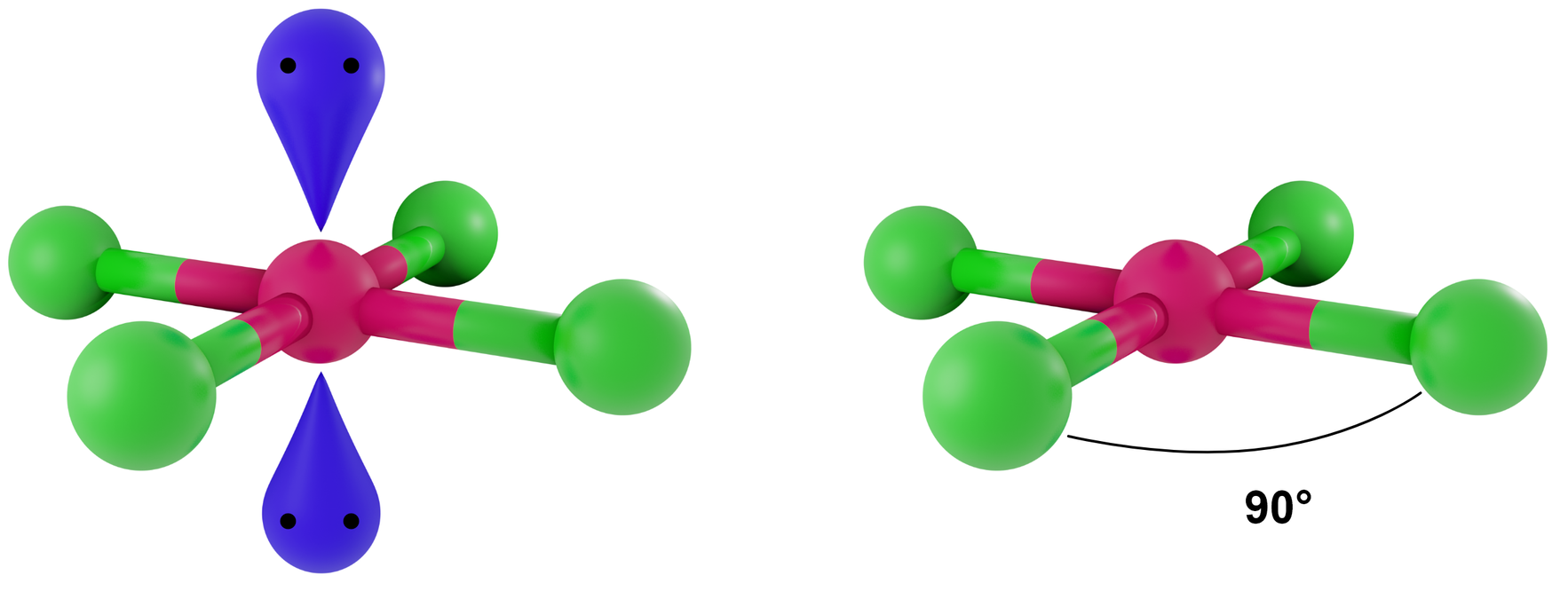
Przykłady: XeF4
Liczba przestrzenna 7, symetria kierunków orbitalnych bipiramidy pentagonalnej
- dla LwpE = 0 - bipiramida pentagonalna
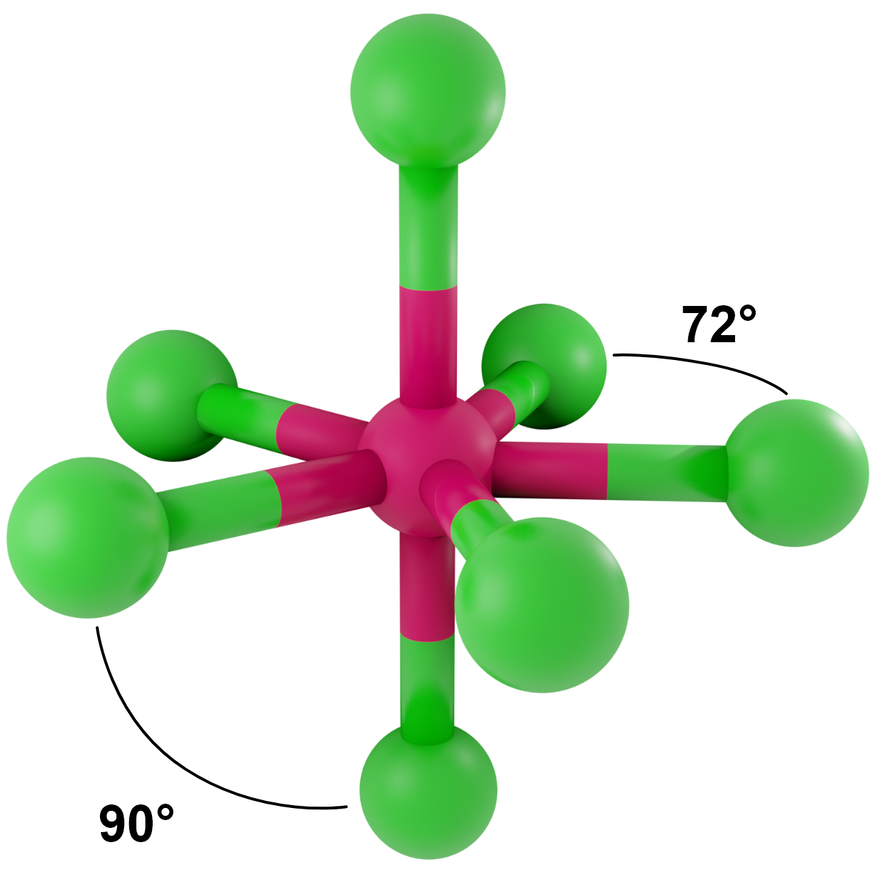
Przykłady: IF7
- dla LwpE = 1 - zdeformowana bipiramida pentagonalna, piramida pentagonalna
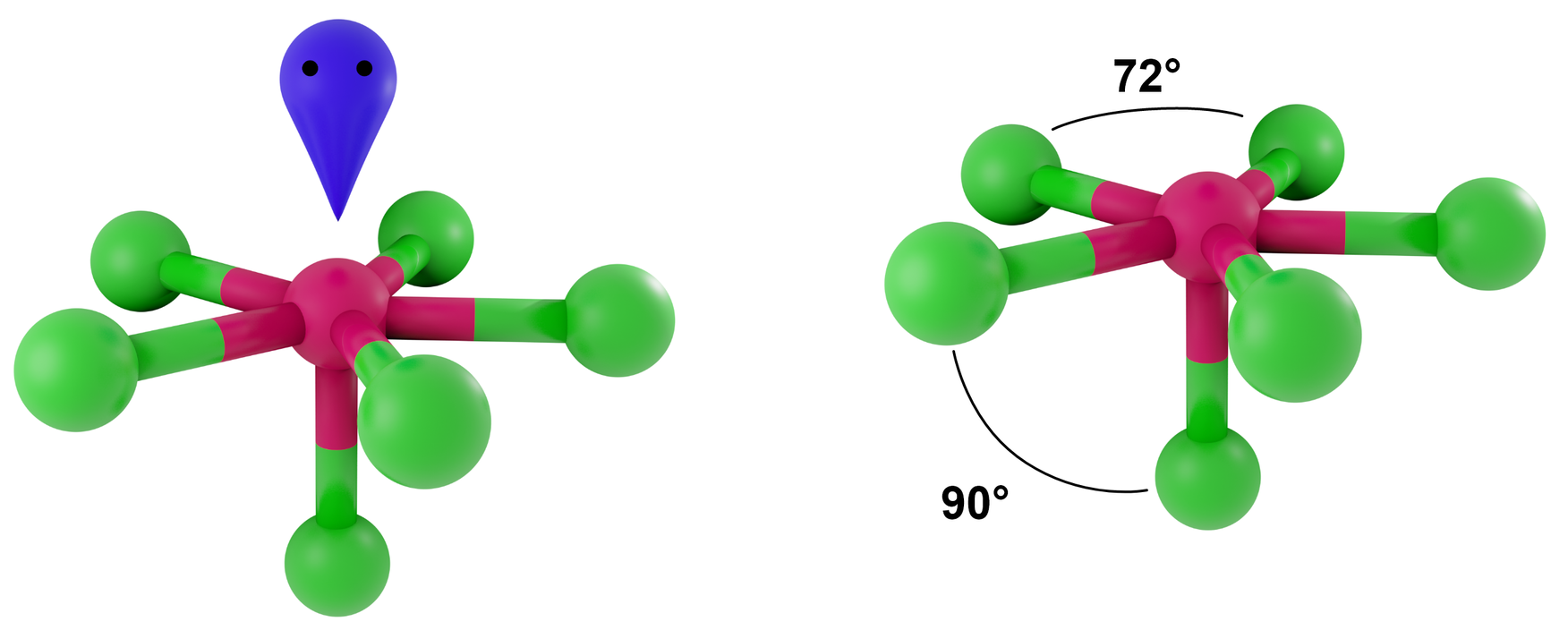
Przykłady: SeBr62-
_________________Grafiki: Kształt cząsteczek lub jonów dla poszczególnych liczb przestrzennych*. Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.
* Wykorzystano grafiki zamieszczone na Zintegrowanej Platformie Edukacyjnej.
1.4. Obliczanie liczby przestrzennej
Poniżej przedstawiona zostanie jedna z możliwych procedur wyznaczania wartości liczby przestrzennej.
Wyznaczenie liczby przestrzennej dla drobiny opisanej wzorem EAnHm na podstawie obliczeń wartości kolejnych parametrów:
LwpE - liczba wolnych par elektronowych atomu centralnego opisana wzorem: LwpE = 1/2 Lwal - 4n - m
Lp - liczba przestrzenna obliczana ze wzoru: Lp = LwpE + n + m
Przykład 1. Cząsteczka CO2 (EAnHm → CO2H0)
LwpE = 1/2 Lwal - 4n - m = 1/2 · 18 - 4 · 2 - 0 = 0
Lp = LwpE + n + m = 0 + 2 + 0 = 2
Symetria kierunków orbitalnych - liniowa (digonalna)
Przykład 2. Jon NH4+ (EAnHm → NA0H4)
LwpE = 1/2 Lwal - 4n - m = 1/2 · 8 - 4 · 0 - 4 = 0
Lp = LwpE + n + m = 0 + 0 + 4 = 4
Symetria kierunków orbitalnych - tetraedryczna
Przykład 3. Jon CO32- (EAnHm → CO3H0)
Symetria kierunków orbitalnych - trygonalna
 Zamieszczony film „Jak przewidzieć kształt cząsteczki?*” przedstawia inną z procedur obliczania liczby przestrzennej.
Zamieszczony film „Jak przewidzieć kształt cząsteczki?*” przedstawia inną z procedur obliczania liczby przestrzennej.
Film: Jak przewidzieć kształt cząsteczki?*. Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.
_________________
* Wykorzystano grafiki zamieszczone na Zintegrowanej Platformie Edukacyjnej.

2. Hybrydyzacja
Hybrydyzacja orbitali jest działaniem matematycznym polegającym na dodawaniu funkcji falowych opisujących elektrony walencyjne tego samego atomu, należące do różnych podpowłok tej samej powłoki. Jako efekt zmieszania orbitali różnego typu uzyskuje się tzw. hybrydy. Hybrydyzację była stosowana jako metoda obliczania i przewidywania właściwości cząsteczek, obecnie ma już jedynie znaczenie historyczne.
 Obejrzyj film, który przybliży Ci "Co to jest hybrydyzacja?”*.
Obejrzyj film, który przybliży Ci "Co to jest hybrydyzacja?”*.
Film: Co to jest hybrydyzacja?*. Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.
Poniżej przedstawiono najpopularniejsze typy hybrydyzacji. Należy wskazać, iż suma indeksów w zapisie symbolu hybrydyzacji jest równa odpowiedniej liczbie przestrzennej, np.: sp2 (1+2=3) → Lp=3.
Typy hybrydyzacji:
- sp – hybrydyzacja digonalna (1+1=2) → Lp=2
 Przykłady: BeH2
Przykłady: BeH2
- sp2 – hybrydyzacja trygonalna (1+2=3) → Lp=3
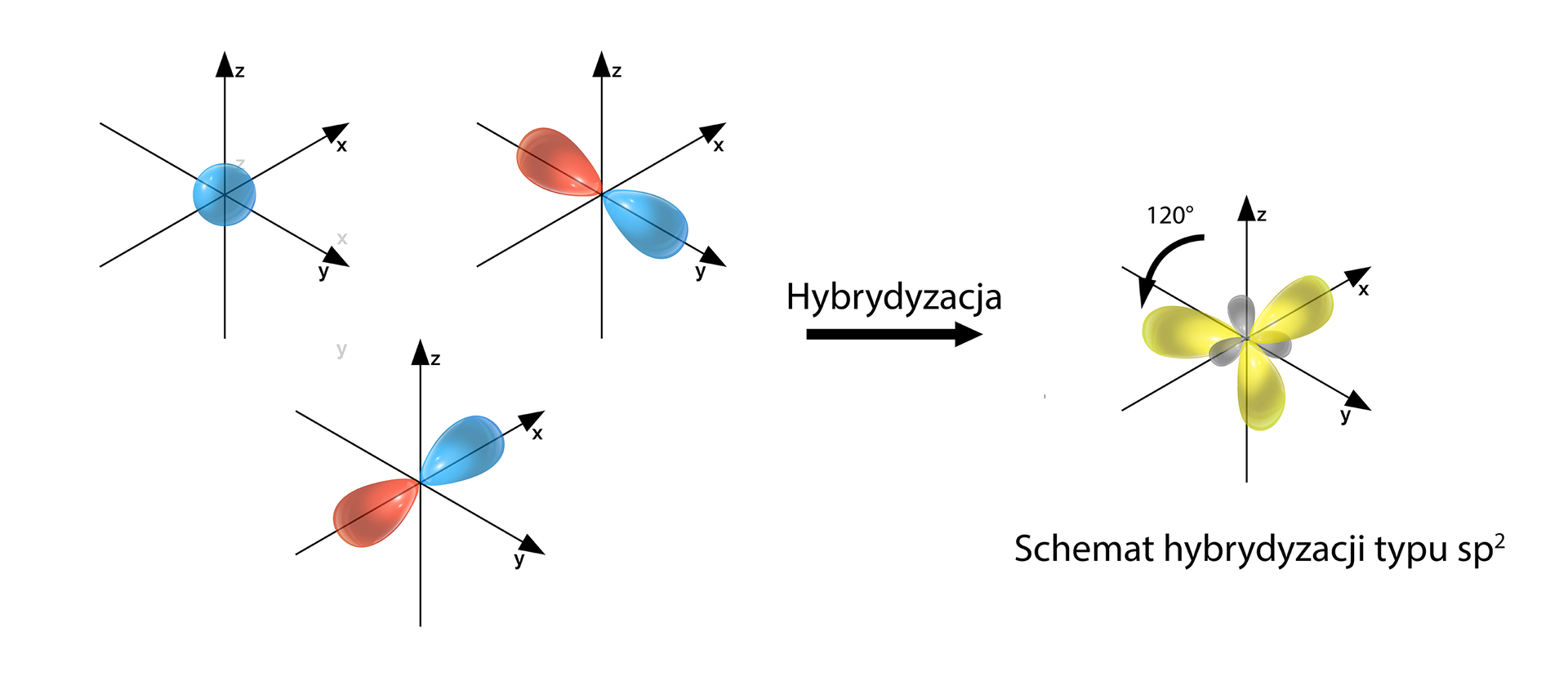 Przykłady: BH3
Przykłady: BH3
- sp3 – hybrydyzacja tetraedryczna (1+3=4) → Lp=4
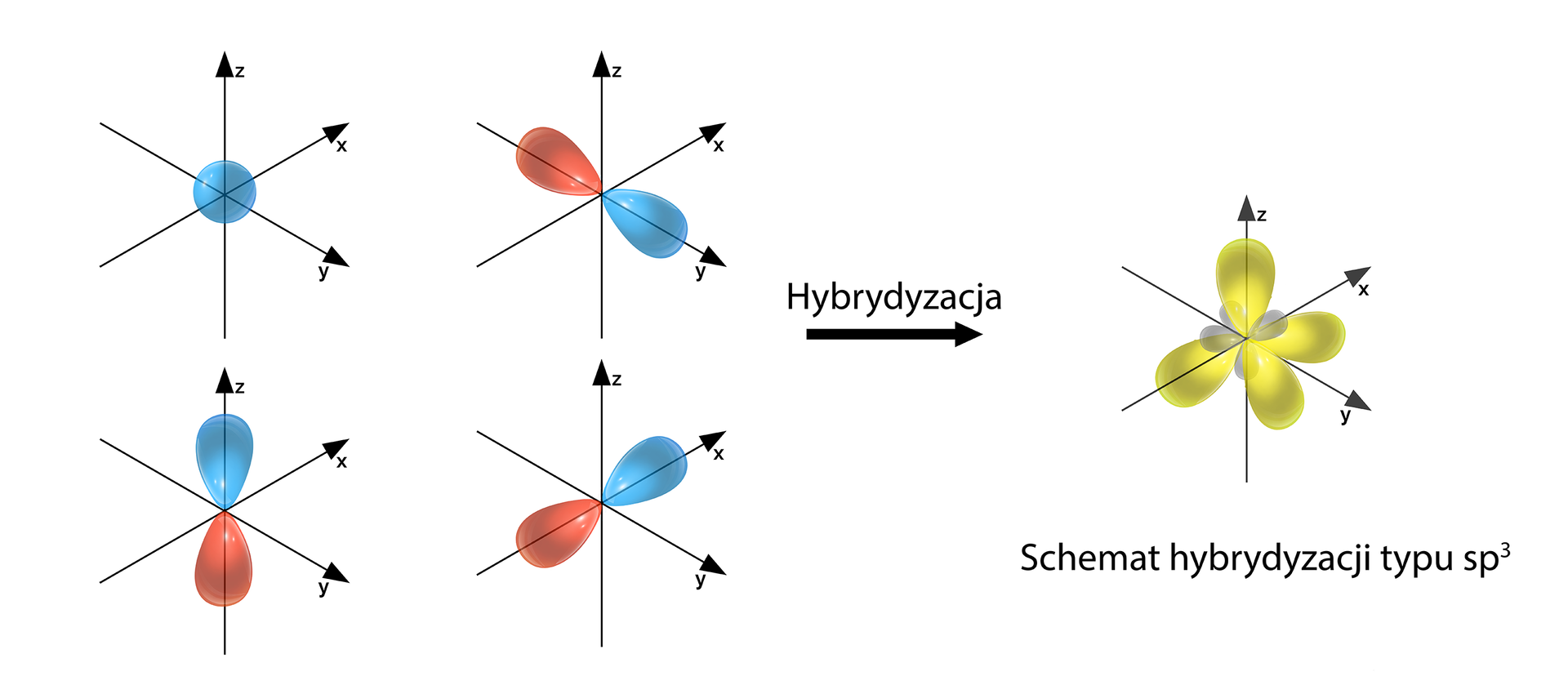
Przykłady: CH4
Grafiki: Schematy hybrydyzacji typu sp, sp2 i sp3*. Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.
Po przeanalizowaniu powyższych przykładów nasuwa się pytanie: Czy orbitale d też mogą brać udział w hybrydyzacji?
Hybrydyzacji mogą ulegać orbitale walencyjne podpowłoki typu s, p i d. W zależności od liczby i typu orbitali typu d biorących udział w hybrydyzacji, można wyróżnić kilka rodzajów hybrydyzacji:
sp3d - hybrydyzacja pentagonalna (1+3+1=5) → Lp=5
Przykłady: PCl5, SF4, ClF3, I3-
sp3d2 - hybrydyzacja heksagonalna (1+3+2=6) → Lp=6
Przykłady: SeF6, ClF5, XeF4
sp3d3 - hybrydyzacja heptagonalna (1+3+3=7) → Lp=7
Przykłady: IF7
 Dla lepszego zobrazowania wyniku działania hybrydyzacji w zakresie mieszania orbitali s, p i d zamieszczono animację "Czy orbitale typu d mogą ulegać hybrydyzacji?”*.
Dla lepszego zobrazowania wyniku działania hybrydyzacji w zakresie mieszania orbitali s, p i d zamieszczono animację "Czy orbitale typu d mogą ulegać hybrydyzacji?”*.
Animacja: Czy orbitale typu d mogą ulegać hybrydyzacji?”*. Źródło: GroMar Sp. z o.o., Dominika Kruszewska, licencja: CC BY-SA 3.0.
_________________
* Wykorzystano grafiki zamieszczone na Zintegrowanej Platformie Edukacyjnej.

3. Bibliografia
Adam Bielański, Podstawy chemii nieorganicznej. Warszawa : Wydawnictwo Naukowe PWN, 2013.
Robert Gill, Chemical Fundamentals of Geology and Environmental Geoscience. Sussex : Wiley-Blackwell, 2015.
Krzysztof M. Pazdro, Anna Rola-Noworyta, Chemia. Repetytorium dla przyszłych maturzystów i studentów. Warszawa : Oficyna Edukacyjna Krzysztof Pazdro, 2014.
Dariusz Witowski, Jan S. Witowski, Chemia - zbiór zadań wraz z odpowiedziami - tom 1-4 (2002-2019) dla kandydatów na uniwersytety medyczne i kierunki przyrodnicze zdających maturę z chemii. Łańcut : Oficyna Wydawnicza "Nowa Matura".
Ikona (źródło): Reshot