Kształt cząsteczek

Liczba przestrzenna 2, symetria kierunków orbitalnych liniowa (diagonalna), L_wpE = 0

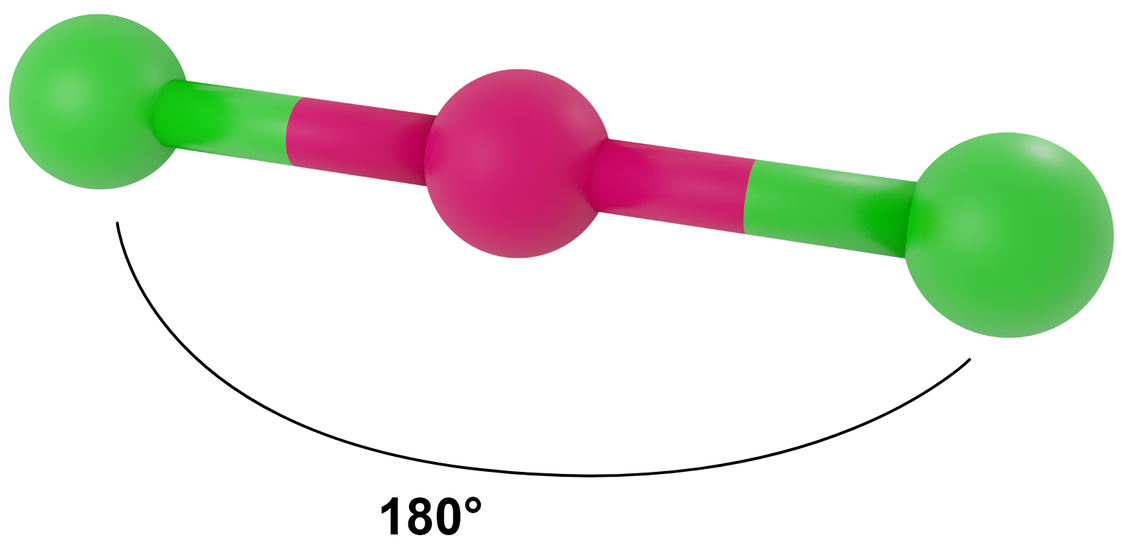
Przykłady: BeCl₂, CO₂

Liczba przestrzenna 3, symetria kierunków orbitalnych trygonalna

• dla L_wpE = 0 - trójkąt równoboczny

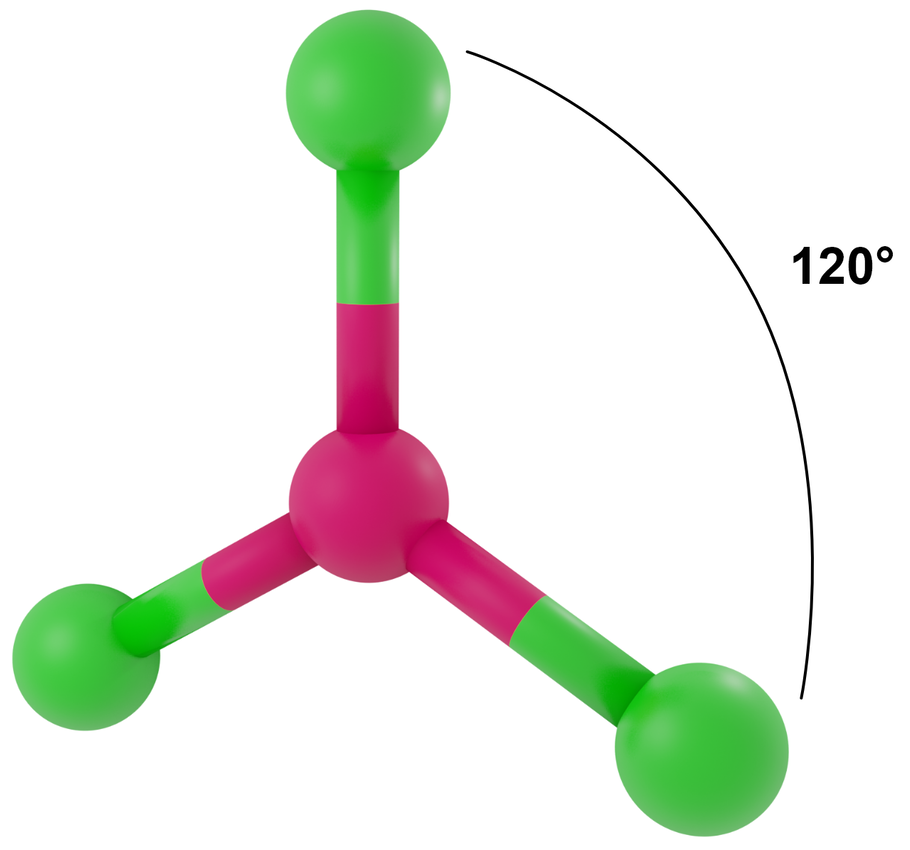
Przykłady: BF₃, CO₃^2-, NO₃^-, SO₃

• dla L_wpE = 1 - trójkąt równoramienny

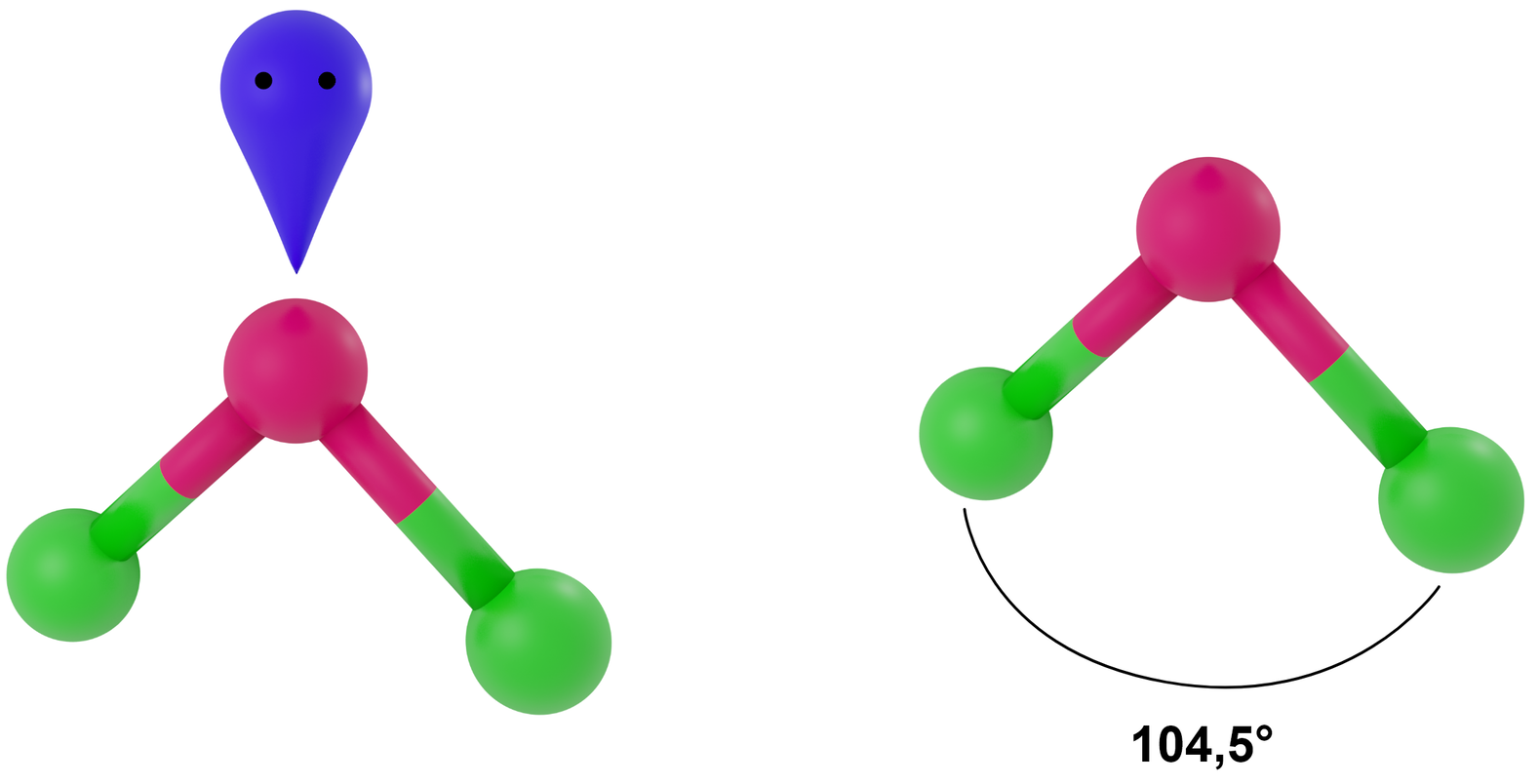
Przykłady: NO₂^-, SO₂, O₃

Liczba przestrzenna 4, symetria kierunków orbitalnych tetraedryczna

• dla L_wpE = 0 - tetraedr

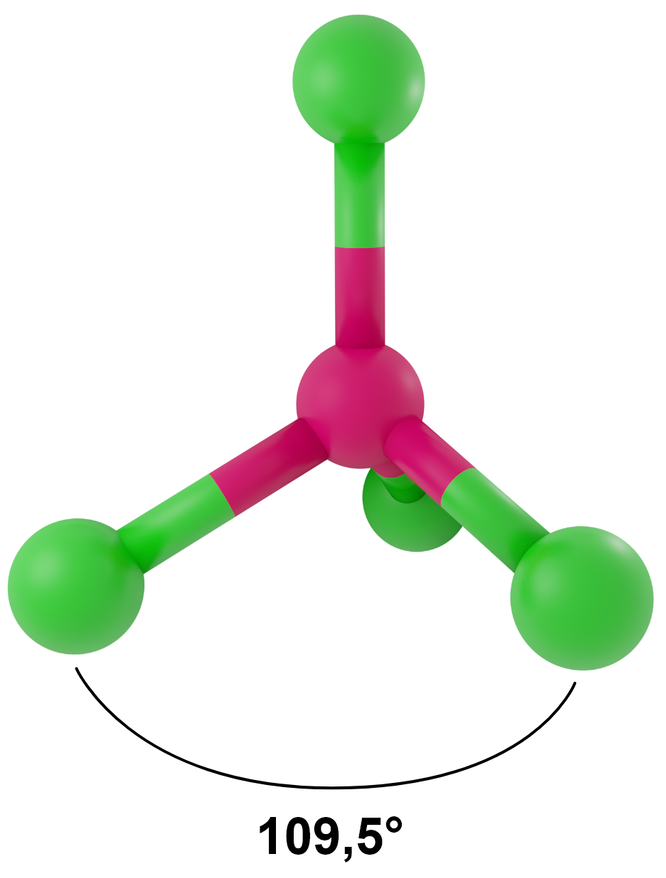
Przykłady: CH₄, PO₄^3-, SO₄^2-, ClO₄^-

• dla L_wpE = 1 - piramida trygonalna

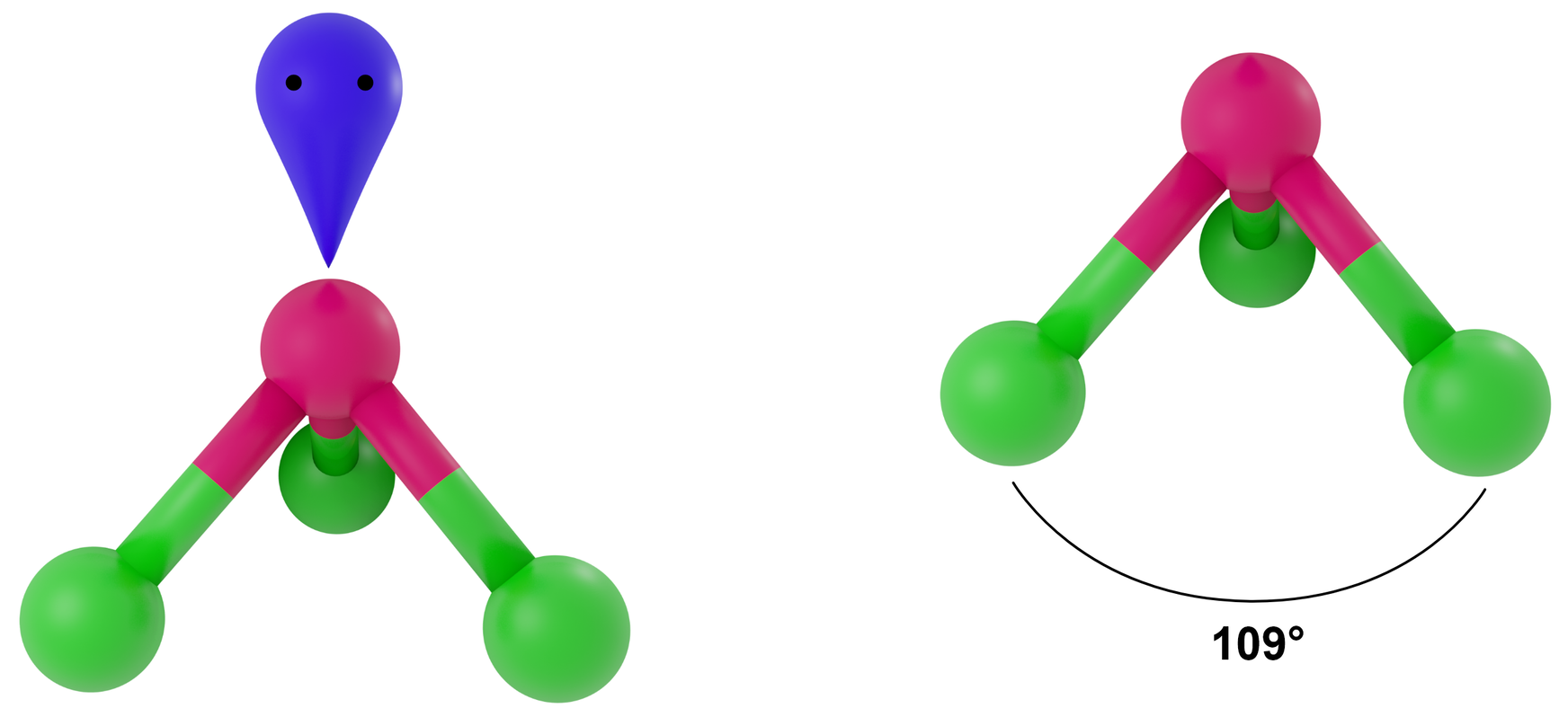
Przykłady: NH₃, PCl₃

• dla L_wpE = 2 - trójkąt równoramienny

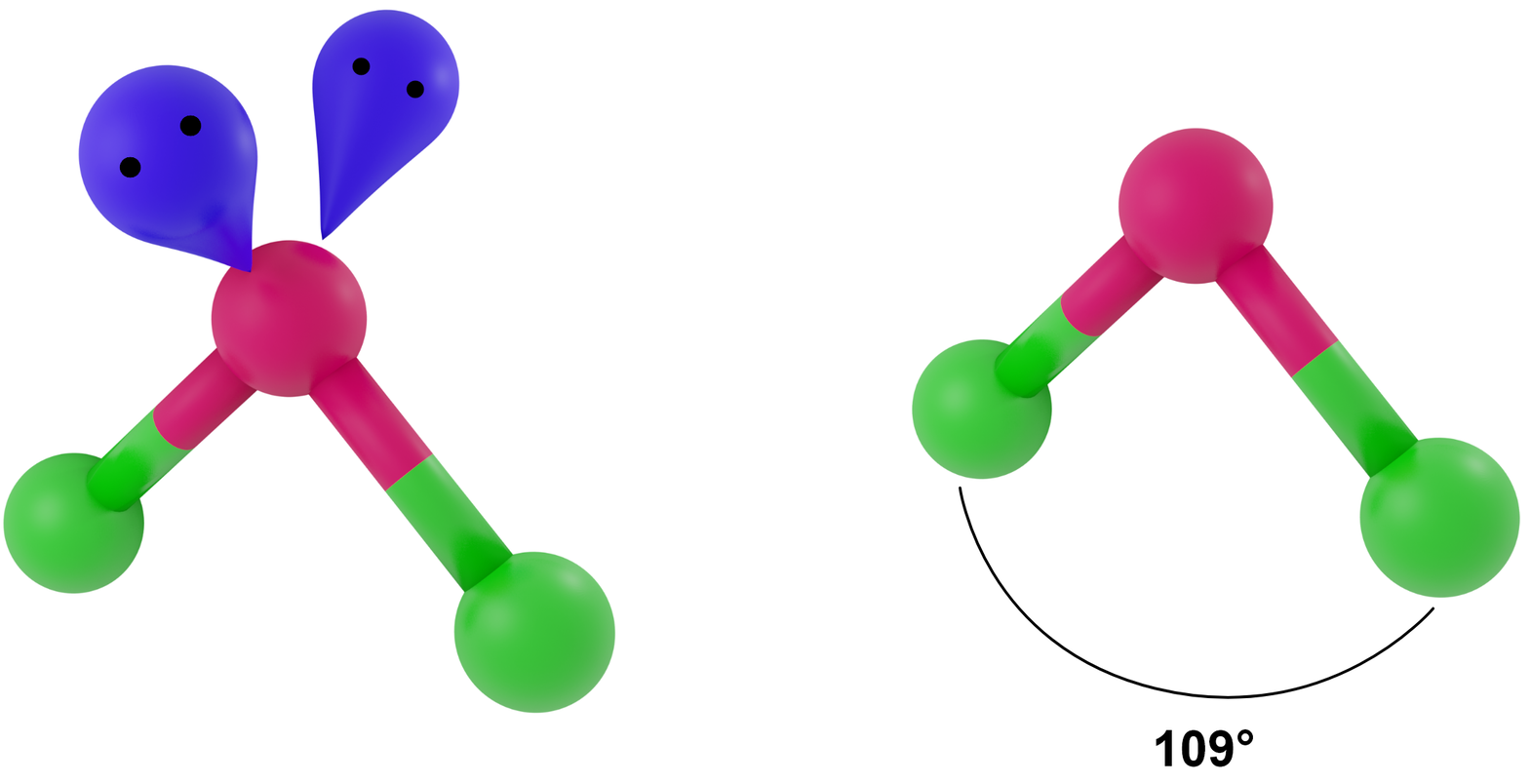
Przykłady: H₂O, OF₂

Liczba przestrzenna 5, symetria kierunków orbitalnych bipiramidy trygonalnej

• dla L_wpE = 0 - bipiramida trygonalna

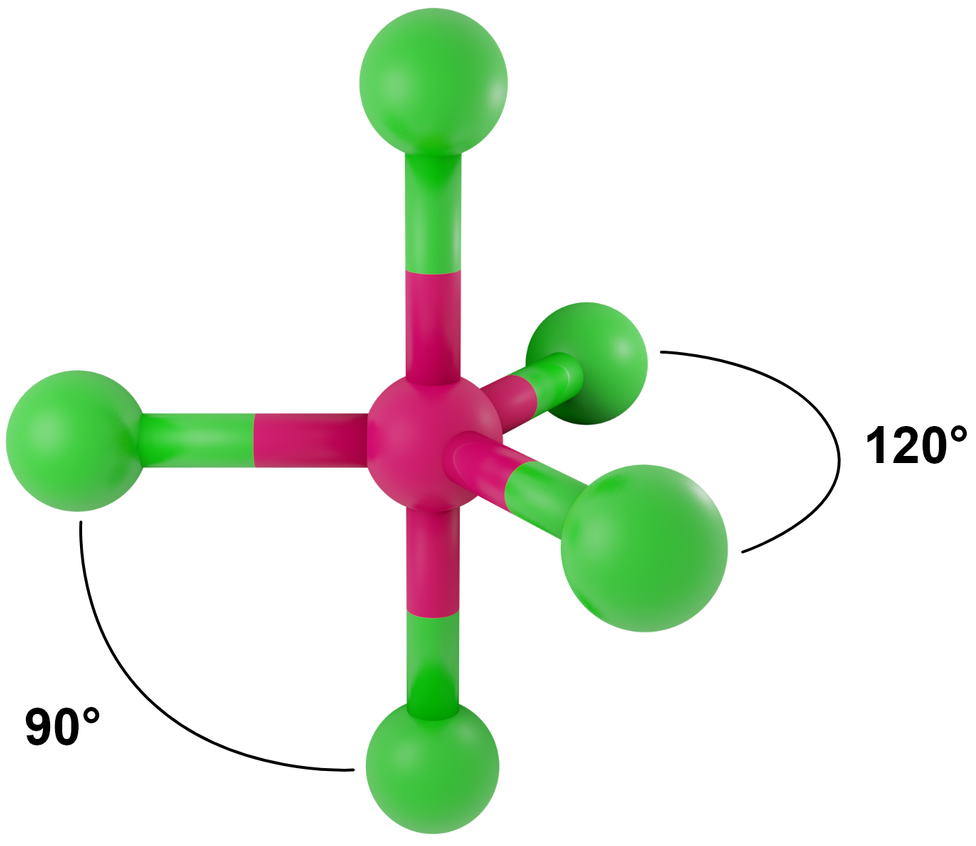
Przykłady: PCl₅

• dla L_wpE = 1 - zdeformowany tetraedr

Przykłady: SF₄

• dla L_wpE = 2 - deltoid wypukły

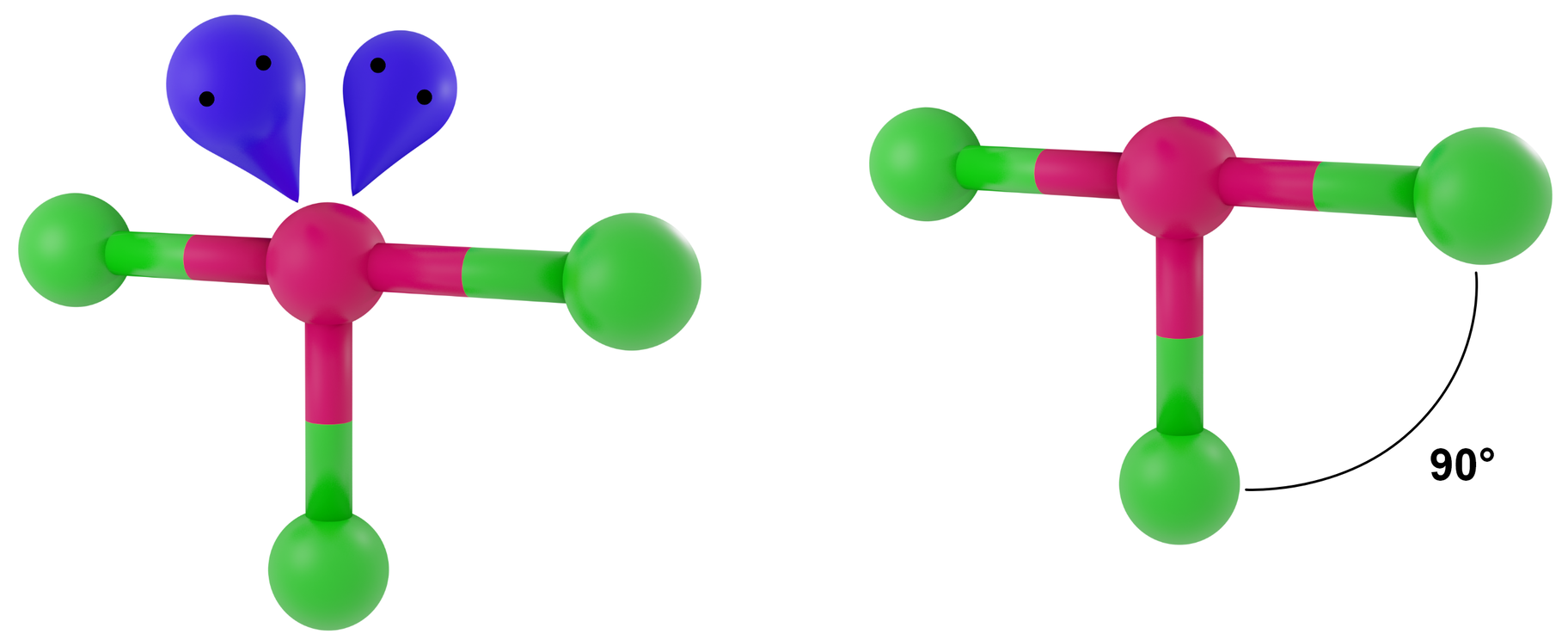
Przykłady: ClF₃, BrF₃

• dla L_wpE = 3 - liniowa

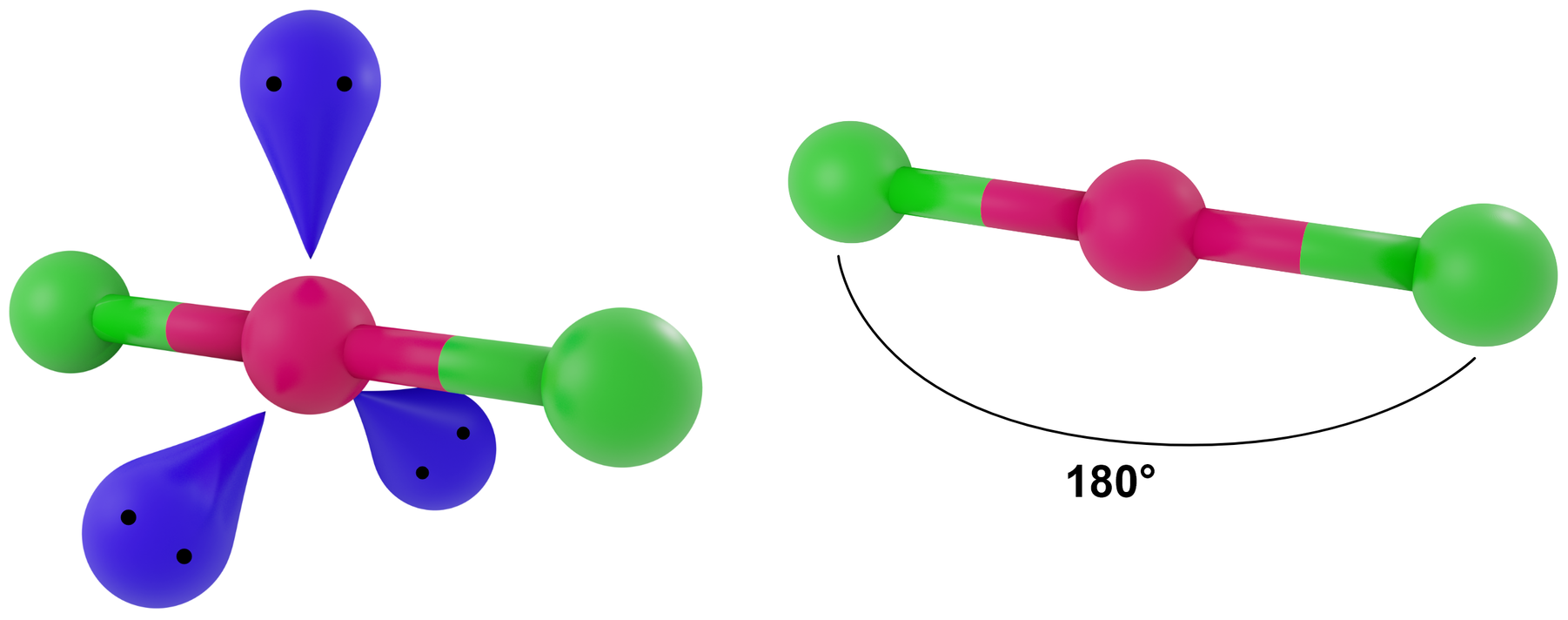
Przykłady: XeF₂, ICl₂^-

Liczba przestrzenna 6, symetria kierunków orbitalnych bipiramidy tetragonalnej (oktaedru)

• dla L_wpE = 0 - bipiramida tetragonalna (oktaedr)

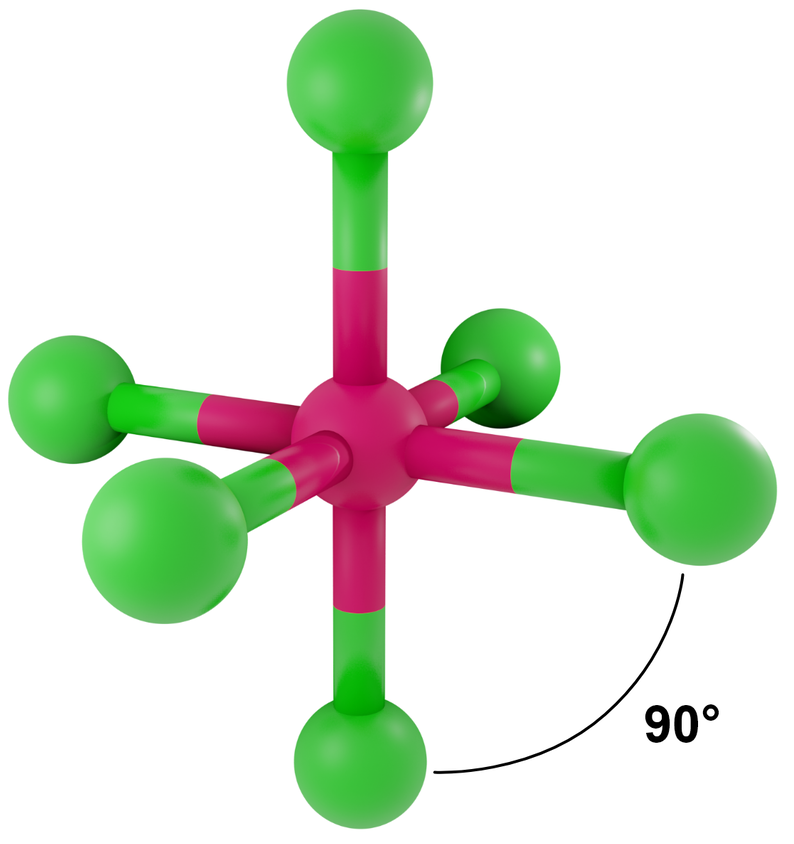
Przykłady: SF₆

• dla L_wpE = 1 -  piramida tetragonalna

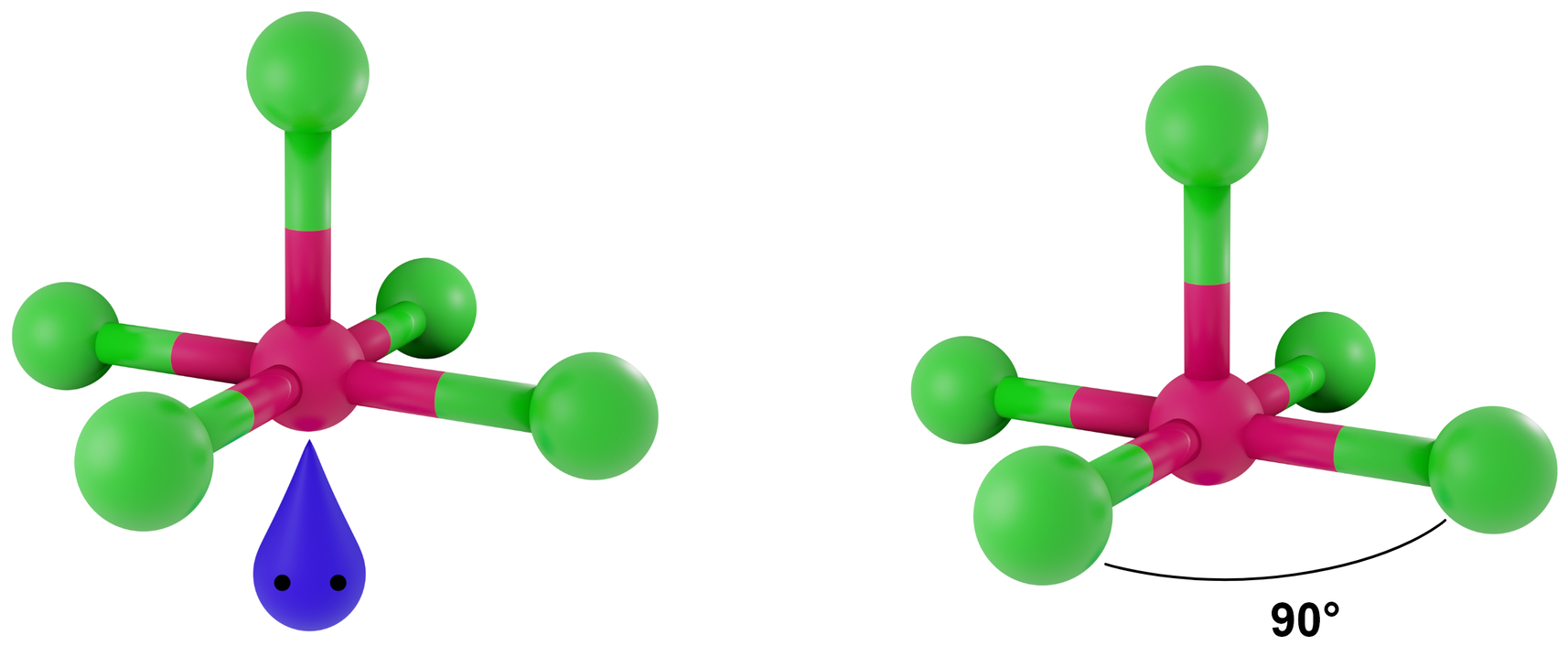
Przykłady: IF₅

• dla L_wpE = 2 -  kwadrat

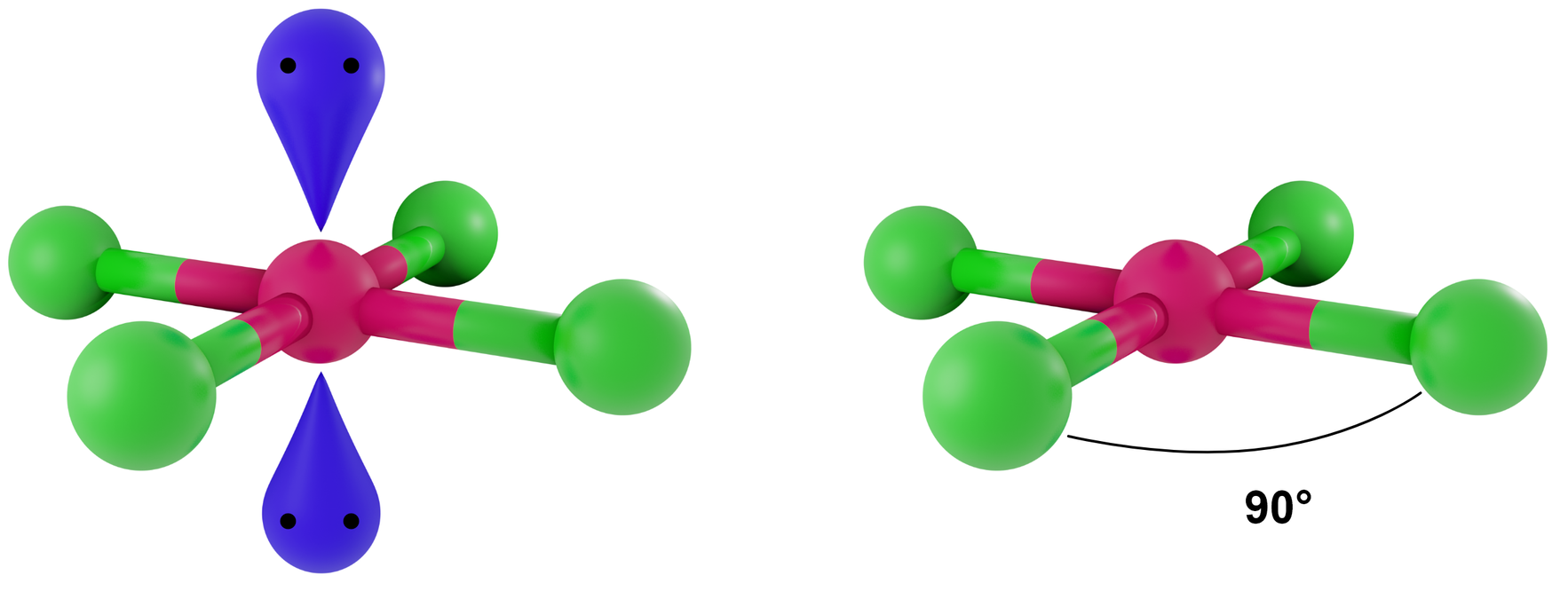
Przykłady: XeF₄ 

Liczba przestrzenna 7, symetria kierunków orbitalnych bipiramidy pentagonalnej

• dla L_wpE = 0 - bipiramida pentagonalna

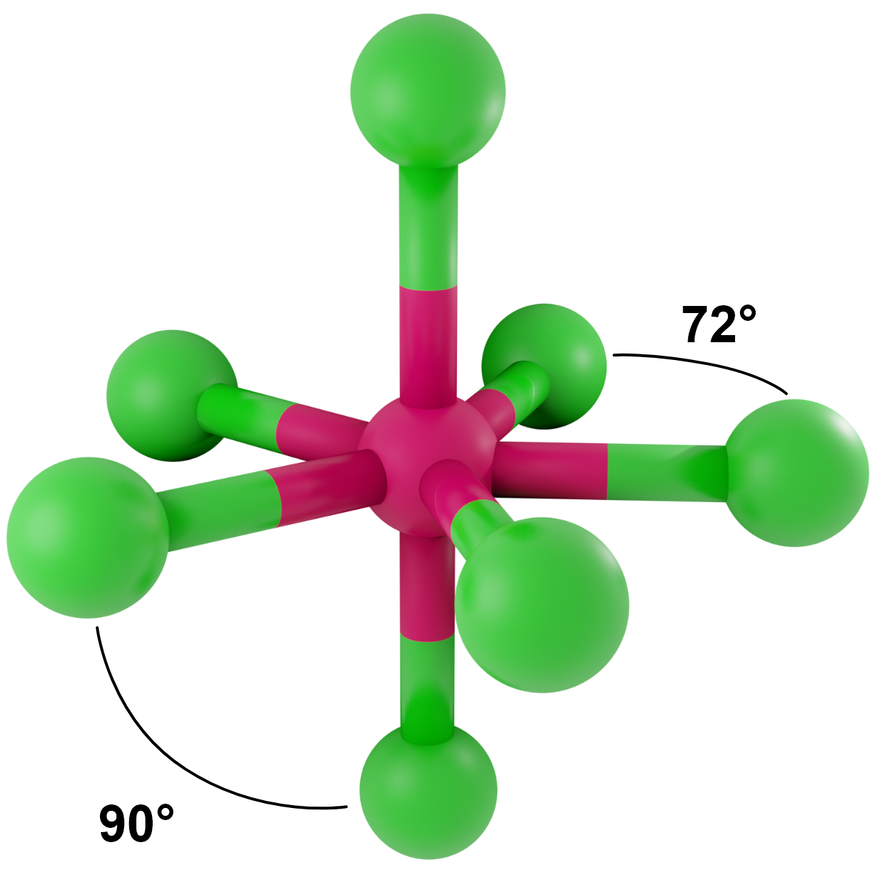
Przykłady: IF₇

• dla L_wpE = 1 - zdeformowana bipiramida pentagonalna, piramida pentagonalna

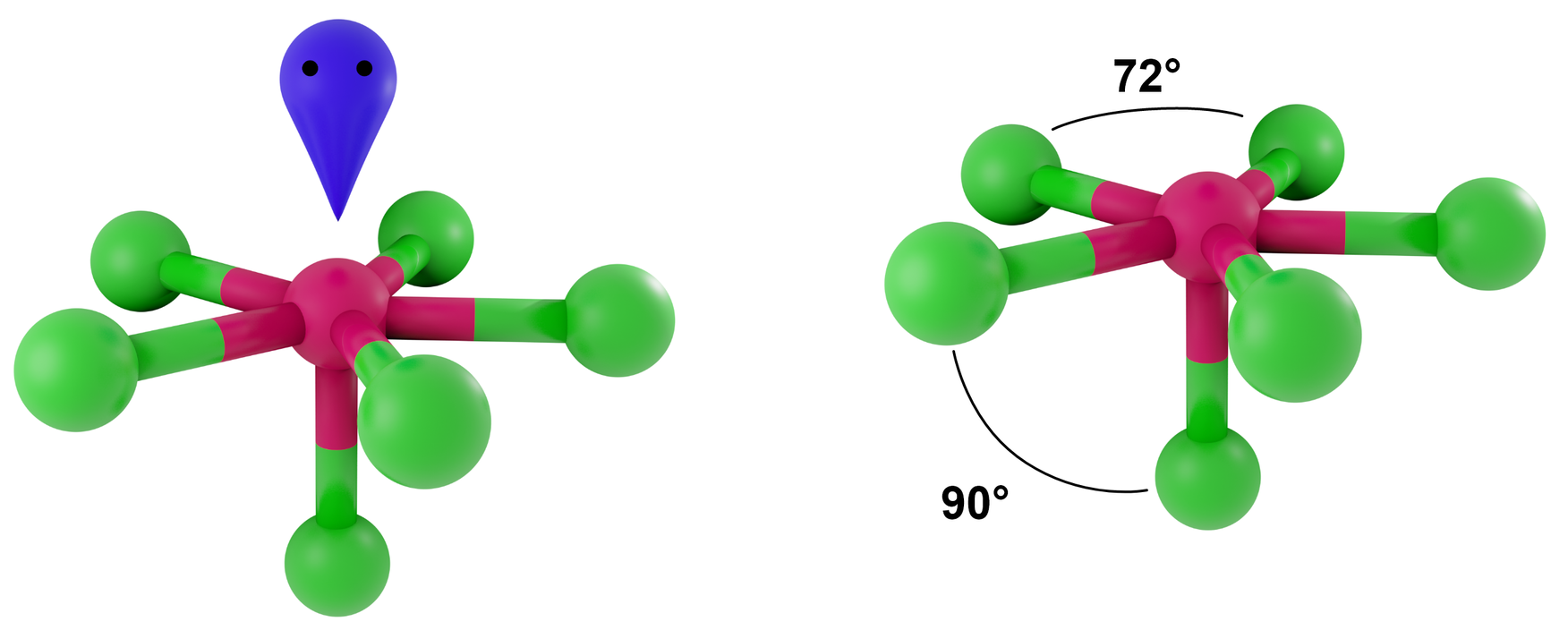
Przykłady: SeBr₆^2-

Grafiki: Kształt cząsteczek lub jonów dla poszczególnych liczb przestrzennych*. 
Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

_________________
* Wykorzystano grafiki zamieszczone na Zintegrowanej Platformie Edukacyjnej.