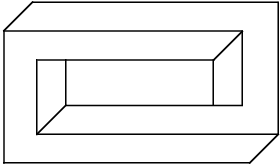
Today's focus - Math: Learn about impossible shapes.
A form is called impossible when our mind tries to interpret it as a three-dimensional object in Euclidean space, with straight edges and planar faces, instead of interpreting it as a two-dimensional object drawn on the paper plane.
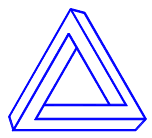
A family of impossible figures studied by knot theory, by Corinne Cerf
The 2D drawing above is not impossible, but our three-dimensional interpretation of it is. As our visual system automatically assigns depth to each point in an image. given the chance to interpret a drawing or image as three-dimensional, we will.
The Generic View Principle is our assumption that we are viewing images from a generic, or general, view. According to The Generic View Principle:
- Two-dimensional straight lines should be interpreted as three-dimensional straight lines.
- Two-dimensional parallel lines should be interpreted as three-dimensional parallel lines.
- Continuous straight lines are interpreted as continuous straight lines.
- Acute and obtuse angles are interpreted as 90° angles in perspective.
- External lines are viewed as the boundary of the shape.
What this means is that our visual system assumes that we are viewing something from a non-accidental point of view, and we believe what we see unless there is information to the contrary.
Penrose Polygons
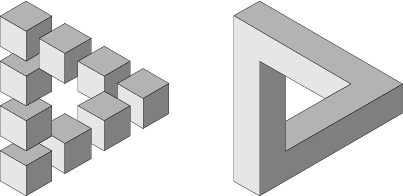
The Penrose triangle, or tribar , tri-bar, impossible tribar, or impossible triangle is comprised of three orthogonal rods, that when viewed from one direction and distance, create the illusion of a triangle. The impossible figure was rediscovered, analyzed, published and popularized by physicist Roger Penrose and his father Lionel Penrose in their article "Impossible Objects: A Special Type of Visual Illusion" from the 1958 edition of the British Journal of Psychology.
Some Background Information
Continuity is defined when the endpoints of two curves meet. The image below shows four possible types of continuity:
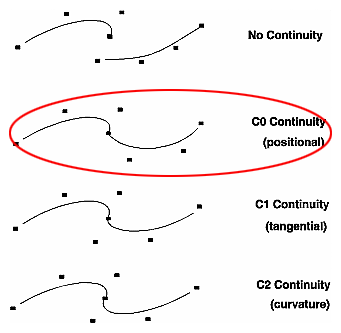
from The Inventor Mentor: Programming Object-Oriented 3D Graphics with Open Inventorâ„¢, Release 2
Swept Surfaces are created by two curves C1(u) and C2(v). The swept surface is the surface generated by moving curve C1(v) along curve C2(u). The curve C1(v) may be rotated and scaled, so for each t in the domain of curve C2(v), curve C1(u) is moved to the point C2(t), with possible rotation and/or scaling. Therefore, as t changes from 0 to 1, the transformed curve C1(u) sweeps out a surface. Under this definition, curves C1(u) and C2(v) are referred to as the profile curve and trajectory curve.

from The Inventor Mentor: Programming Object-Oriented 3D Graphics with Open Inventorâ„¢, Release 2
Swept Surfaces are created by two curves C1(u) and C2(v). The swept surface is the surface generated by moving curve C1(v) along curve C2(u). The curve C1(v) may be rotated and scaled, so for each t in the domain of curve C2(v), curve C1(u) is moved to the point C2(t), with possible rotation and/or scaling. Therefore, as t changes from 0 to 1, the transformed curve C1(u) sweeps out a surface. Under this definition, curves C1(u) and C2(v) are referred to as the profile curve and trajectory curve.
A triangle swept along straight path yields wedge
A circle along a straight path results in cylinder
A circle of decreasing radius results in a cone
Rotation along with sweep can be combined to give a twist to the generated surface
The Impossible Torus demonstrates sweeping a square shape along a circle trajectory, while the square is rotated. The four instances of the impossible torus differ from each other only by the amount the square cross section is rotated while swept along the 360 degrees of the circle, starting from 90 degrees rotation on the left, all the way to 360 degree in the right example.




The shapes below are constructed as a C0 continuous sweep surface with a square cross section that rotates as it moves along the edges.
Front View

General View


General View

Downloads
stl of a Penrose triangle by Gershon Elber

stl of this form

by
Tribox
You can continue to add sides to create arbitrary Penrose n-gons.
Downloads
stl of this form

by
Hex Nut
The hex nut is another example of an impossible shape. Here again, one can construct a real 3D object that from a certain view will look like the impossible hex nut. 
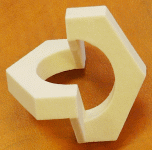
Escher's (Louis Albert Necker's Cube)
The Necker cube is an ambiguous line drawing that was first published as a rhomboid in 1832 by Swiss crystallographer Louis Albert Necker.Front View

General View