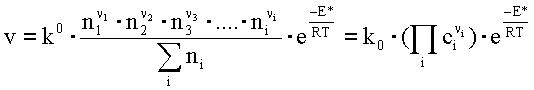1.3   Teoria zderzeń jako statystyczny opis procesu chemicznego. Równanie  kinetyczne. 

Aby zaszła reakcja (2.1) pomiędzy cząsteczkami A i B musi dojść do ich kolizji (zderzenia). Nie wszystkie jednak zderzenia prowadzą do powstania nowej cząsteczki AB. Tylko zderzenia cząsteczek o energii równej lub większej niż pewna „progowa” energia E* zwana energią aktywacji prowadzą do reakcji chemicznej i powstania nowej molekuły (zderzenia „aktywne”).

Ilość cząsteczek o energii równej lub większej niż energia aktywacji dana jest rozkładem statystycznym Maxwella-Boltzmanna:

            (3.1)                           

gdzie:

            N* jest ilością cząsteczek o energii większej niż energia aktywacji E*,

            N₀ całkowitą ilością cząsteczek,

k  stałą Boltzmanna (II.2.1.1.3),

T  temperaturą w skali bezwzględnej (Kelwina) (II.2.1.2.3).

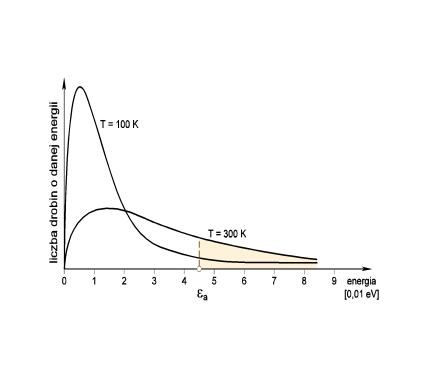
Rys. 3.1 ilustruje rozkład prawdopodobieństwa występowania cząstek o różnej energii E. Obszar zacieniony odpowiada ilości cząsteczek o energii równej lub większej niż energia aktywacji E* dla dwóch temperatur 100K i 300K. 

Szybkość reakcji chemicznej jest proporcjonalna do ilości zderzeń aktywnych, a więc do ilości cząsteczek o energii równej lub większej od energii aktywacji E*:

            (3.2)                                

Jeśli ilość cząsteczek reagujących wyrazimy poprzez  ilość moli n to szybkość reakcji można opisać równaniem:

            (3.3)                           

gdzie:

            jest ilością moli,

n* jest ilością moli cząsteczek o energii większej niż energia aktywacji E*,

            n₀ całkowitą ilością moli danej substancji w układzie,

R = k·N_A jest stałą gazową.

Jeśli w układzie mamy ogólną reakcję:

to szybkość reakcji będzie proporcjonalna do iloczynu stężeń wszystkich cząsteczek  biorących udział w reakcji:

(3.4)           

gdzie:

            n₁, n₂, n₃, ......n_i  moli reagujących cząsteczek A¹,A²,A³,....Aⁱ  składa się na całkowitą ilość moli n₀ ( ), a wartość 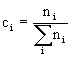    jest stężeniem substancji Aⁱ.

            Wartości  są  współczynnikami stechiometrycznymi.

Równanie (3.4a) nosi nazwę równania kinetycznego reakcji chemicznej:

            (3.4a)                         

gdzie wartość k jest stałą szybkości reakcji:

            (3.5a)                         

Równanie kinetyczne podaje wpływ stężenia reagentów na szybkość reakcji chemicznej.