Symulacje komputerowe z fizyki
Przegląd sekcji
-
Symulacje komputerowe z fizyki
-
-
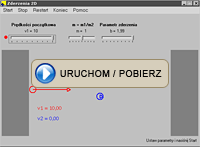
1. Ruch jednostajnie zmienny
Program pozwala śledzić ruch jednostajnie zmienny wzdłuż linii prostej (oś \(x\)). W programie można zmieniać prędkość początkową oraz przyspieszenie. Na wykresach można obserwować zależność położenia ciała, drogi przebytej przez ciało i jego prędkości od czasu.
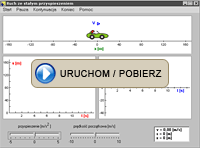
2. Rzut ukośny
Program ilustruje rzut ukośny, tj. ruch na płaszczyźnie, w którym zmienia się wartość i kierunek prędkości. Program pozwala obserwować ruch punktu materialnego w zależności od wartości prędkości początkowej \(v_Q\) oraz kąta wyrzutu. W trakcie ruchu można śledzić prędkość chwilową oraz jej składowe: \(v_x\) (składowa pozioma) i \(v_y\) (składowa pionowa). Można także obserwować przyspieszenie i jego składowe: \(a_n\) (składowa normalna do toru, odpowiedzialna za zmianę kierunku prędkości) oraz \(a_s\) (składowa styczna związana ze zmianą wartości prędkości). Odpowiednie wartości chwilowe prędkości lub przyspieszenia są wyświetlane w okienku na wykresie. Po zakończeniu ruchu ciała wyświetlane są parametry rzutu, min. zasięg i wysokość maksymalna. W programie można porównać cztery wykresy (cztery rzuty).
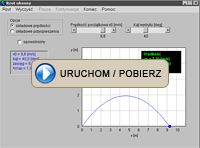
3. Praca wykonana przez siłę zmienną
Ten program nie ilustruje zjawiska fizycznego, ale demonstruje sposób obliczania pracy wykonanej przez zmienną siłę będącą funkcją położenia \(F(x)\) (której kierunek jest zgodny z osią \(x\)) przy przesuwaniu ciała od położenia \(x_1\); do położenia \(x_2\). W programie można podzielić całkowite przemieszczenie na \(n\) jednakowych odcinków \(\Delta x\). Wewnątrz takiego przedziału przyjmujemy (to jest przybliżenie), że siła jest stała i możemy teraz policzyć pracę na tym odcinku. \(\Delta W_i = F_i\Delta x_i\), gdzie \(F_i\) jest wartością siły na tym odcinku. Całkowita praca jest obliczana jako suma prac na kolejnych odcinkach. Od strony czysto formalnej liczenie pracy jest równoważne liczeniu sumy powierzchni prostokątów o szerokości \(\Delta x\) i wysokości \(F_i\). W programie możemy zwiększyć liczbę podziałów odcinka \((x_1, x_2)\) i zobaczyć, jak dzielenie tego przedziału na więcej (mniejszych) odcinków \(\Delta x\) wpływa na dokładność obliczeń pracy wykonanej przez zmienną siłę \(F(x)\), śledząc różnicę pomiędzy polem prostokątów i polem pod krzywą. W końcu dla bardzo dużej liczby podziałów (teoretycznie w granicy \(\Delta x \rightarrow 0\)) otrzymujemy pole powierzchni pod krzywą. Tak w matematyce definiujemy całkę. Całkowanie funkcji \(F(x)\) w zadanych granicach odpowiada liczeniu pola powierzchni pod krzywą \(F(x)\) w zadanym przedziale.
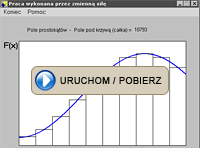
4. Zderzenia centralne
W przypadku zderzeń centralnych, nawet nie znając szczegółów oddziaływania, można, stosując zasadę zachowania pędu oraz zasadę zachowania energii całkowitej, przewidzieć wynik zderzenia. Program pozwala prześledzić wynik zderzenia dwu kuł poruszających się wzdłuż linii łączącej ich środki (zderzenia centralne - jednowymiarowe.) W programie można zmieniać zarówno prędkości początkowe obu kul, jak i ich masy. Można też zmieniać współczynnik restytucji. Jest to empiryczny parametr wyrażający stosunek prędkości względnych ciał po zderzeniu i przed zderzeniem. Dla zderzeń sprężystych parametr ten przyjmuje wartość l, a dla zderzeń całkowicie niesprężystych jest równy 0.
5. Zderzenia sprężyste w dwóch wymiarach
W przypadku zderzeń niecentralnych znajomość mas ciał zderzających się oraz ich prędkości przed zderzeniem NIE wystarcza do wyznaczenia pełnej kinematyki zderzenia. Trzeba znać np. jeden z kątów rozproszenia lub parametr zderzenia \(b\), tj. odległość między pierwotnym kierunkiem ruchu jednego ciała a środkiem drugiego (tarczy). Program pozwala prześledzić wynik sprężystego zderzenia dwu kul w zależności od parametru zderzenia \(b\), prędkości względnej kul i stosunku ich mas.
-
-
-
6. Drgania swobodne
Program ilustruje ruch ciała pod wpływem siły sprężystości (siły harmonicznej) \(F = - ky\), która jest proporcjonalna do przesunięcia y ciała od początku układu i która jest skierowana ku początkowi układu. Program pozwala śledzić ruch masy zamieszonej na nieważkiej sprężynie w zależności od jej współczynnika sprężystości \(k\), masy \(m\) zawieszonej na sprężynie i od amplitudy ruchu \(A\). Na dwóch wykresach wykreślane są zależności czasowe wychylenia \(y(t)\), prędkości \(v(t)\) oraz energii kinetycznej i potencjalnej.
7. Drgania tłumione
W przypadku drgań mechanicznych ciała w ośrodku, oprócz siły sprężystości \(F = -kx\) mamy do czynienia z siłą oporu ośrodka hamującą (tłumiącą) ruch cząstki. Siła oporu ma zwrot przeciwny do prędkości i w najprostszej postaci jest wprost proporcjonalna do prędkości \(F_{op} \sim v\). Współczynnik proporcjonalności nazywany jest współczynnikiem tłumienia \(\beta\). W przypadku „słabego tłumienia" otrzymujemy drgania tłumione okresowo zmienne, w przeciwnym razie ruch nie jest już ruchem drgającym, ale ruchem pełzającym (aperiodycznym).
Program pozwala śledzić ruch wahadła matematycznego w zależności od wielkości tłumienia. W programie można zmieniać wartość współczynnika tłumienia, jak i długość wahadła i amplitudę drgań. Można obserwować ruch drgający tłumiony lub pełzający. Na wykresie można porównać dwa przebiegi wychylenia od czasu.
8. Składanie ruchów falowych
Program pozwala obserwować wynik nakładania się dwóch poprzecznych fal harmonicznych. W programie można zmieniać stosunek amplitud interferujących fal oraz ich różnicę faz. Dobierając te parametry, możemy prześledzić, jakie warunki muszą być spełnione np. dla maksymalnego wzmocnienia lub całkowitego wygaszenia się fal. Oprócz interferencji w przestrzeni (dodawanie fal o tej samej częstości) możemy prześledzić przypadek interferencji w czasie. Pojawia się ona, gdy przez dany punkt w przestrzeni przebiegają w tym samym kierunku fale o trochę różnych częstotliwościach, co możemy zrealizować w programie, zmieniając stosunek częstotliwości. Mamy wówczas do czynienia z modulacją amplitudy \(AM\). Dla fal dźwiękowych \(AM\) przejawia się jako zmiana głośności nazywana dudnieniami. Wreszcie możemy zaobserwować wynik nakładania się dwóch identycznych fal poruszających się w przeciwnych kierunkach (np. fala padająca i odbita). Otrzymana fala wypadkowa nazywana jest falą stojącą i charakteryzuje się tym, że amplitudy drgań poszczególnych punktów ośrodka zależą od ich położeń. W programie możemy obserwować fale składowe, falę wypadkową lub wszystkie te fale.
9. Efekt Dopplera
Zjawisko Dopplera polega na pozornej zmianie częstotliwości fal wysyłanych przez źródło, w wyniku względnego ruchu odbiornika (obserwatora) i źródła. W programie pokazany jest efekt Dopplera dla fal dźwiękowych i dla przypadku ruchu źródła i obserwatora wzdłuż łączącej ich linii prostej. Program pozwala prześledzić zmiany częstotliwości odbieranych fal w zależności od prędkości źródła i odbiornika. W programie można zmieniać zarówno wartość prędkości, jak i jej znak, tj. kierunek ruchu (w prawo lub lewo). Można też zmieniać częstotliwość drgań własnych źródła. Wybierając różne opcje, można prześledzić zmiany częstotliwości, w przypadku gdy źródło i odbiornik zbliżają się do siebie, oddalają się od siebie lub gdy mijają się (zbliżanie i oddalanie się). Porównanie częstotliwości fali wysyłanej ze źródła i odbieranej przez odbiornik jest możliwe dzięki rejestracji impulsów. Każdorazowo, gdy impuls zostaje wysłany ze źródła, jest on rejestrowany: pojawia się znacznik w lewym panelu - impulsy wysłane. Podobnie, gdy impuls dotrze do odbiornika, zostaje zarejestrowany: pojawia się znacznik w prawym panelu - impulsy odebrane.
-
-
-
10. Rozkład Maxwella prędkości cząsteczek
Każdy gaz ma charakterystyczny rozkład prędkości, który zależy od temperatury (cząstki nie mogą mieć takich samych prędkości, bo prędkości zmieniają się w wyniku zderzeń). C. Maxwell podał prawo rozkładu prędkości cząsteczek w danej temperaturze. Program pozwala śledzić zależność tego rozkładu od temperatury. W programie można zapamiętać (zapisać) rozkład prędkości (dla danej temperatury) celem porównania go z rozkładem dla innej temperatury. Na wykresie zaznaczone są: prędkość średnia, prędkość średnia kwadratowa oraz prędkość najbardziej prawdopodobna.
11. Dyfuzja
Zjawisko dyfuzji polega na samorzutnym przechodzeniu cząsteczek w kierunku obszarów o mniejszej koncentracji (stężeniu). Ten proces wyrównywania koncentracji w układzie spowodowany jest chaotycznym ruchem cieplnym cząsteczek i zderzeniami pomiędzy nimi. To właśnie dyfuzja umożliwia mieszanie się substancji pozostających w fazie gazowej lub ciekłej. Efektem jest wyrównywanie się koncentracji wszystkich składników w całej objętości. Program pozwala obserwować mieszanie się dwóch gazów, znajdujących się początkowo w oddzielnych zbiornikach, w zależności od ich temperatury. W programie można śledzić na bieżąco zmiany koncentracji gazów. Ponadto pokazany jest rozkład prędkości cząsteczek gazu wraz z podaną przez Maxwella funkcją rozkładu prędkości (linia ciągła) cząsteczek gazu doskonałego.
-
-
-
12. Elektrostatyka
Kierunek pola \(E\) w przestrzeni można przedstawić graficznie za pomocą tzw. linii sił (linii pola). Są to linie, do których wektor \(E\) jest styczny w każdym punkcie. Linie sił zaczynają się zawsze na ładunkach dodatnich, a kończą na ładunkach ujemnych. Podobnie jak natężenie pola elektrycznego, również potencjał elektryczny można przedstawić graficznie. W tym celu rysujemy powierzchnie lub linie ekwipotencjalne, które przedstawiają w przestrzeni zbiory punktów o jednakowym potencjale. Program pozwala wyznaczyć linie sił pola elektrycznego i rozkład potencjału pochodzący od zadanego statycznego rozkładu ładunków. W programie można wybrać jeden z proponowanych układów ładunków (np. dipol) lub utworzyć własny układ ładunków. Maksymalnie można umieścić na wykresie 12 ładunków. Wybierając opcję „Auto" można automatycznie wygenerować rozkład linii lub wprowadzać pojedyncze linie, klikając w wybranych punktach na wykresie po uprzednim zaznaczeniu opcji \(F(r)\). Podobnie można automatycznie wygenerować rozkład potencjału, wybierając opcję \(V(r)\). Opcja „Auto" pozwala wygenerować automatycznie linie stałego potencjału, a opcja \(V = const\). umożliwia tworzenie takich linii w wybranych punktach na wykresie. Składowe pola elektrycznego, wartość potencjału w danym punkcie oraz współrzędne są wyświetlane w panelu „Parametry".
13. Tor ruchu ładunku w polu magnetycznym B
Program pozwala prześledzić tor, po jakim porusza się naładowana cząstka w polu magnetycznym, w zależności od wartości indukcji pola \(B\), wartości prędkości cząstki \(v\) oraz kąta, pod jakim cząstka wpada do pola \(\beta\). W programie można zmieniać również perspektywę (kąt widzenia toru) oraz obracać rysunek tak, aby lepiej zaobserwować tor ruchu cząstki.
14. Wizualizacja fali elektromagnetycznej
Animacja przedstawia spolaryzowaną liniowo falę elektromagnetyczną rozchodzącą się w kierunku \(y\) (Wektory pola elektrycznego są równoległe do osi \(z\), a wektory pola magnetycznego do osi \(x\)). W programie można zmieniać długość fali i amplitudę pól.
15. Obwód szeregowy RLC
Program pozwala śledzić przebiegi czasowe spadków napięć na poszczególnych elementach obwodu R, L, C oraz porównać je z napięciem zasilającym \(U(t)\) i prądem w obwodzie \(I(t)\) .Parametry układu: R, L, C oraz częstotliwość napięcia wymuszajacego f można zmieniać, w zadanym zakresie, za pomocą odpowiednich suwaków. W szczególności można tak dobrać częstotliwość f napięcia zasilania lub częstotliwość własną obwodu (zmieniając L i C) aby zaobserwować zjawisko rezonansu napięć.
-
-
-
16. Odbicie i załamanie światła
Program demonstruje bieg promieni świetlnych przy przejściu przez płaską powierzchnię rozgraniczającą dwa ośrodki w zależności od kąta padania światła na powierzchnię graniczną i od współczynników załamania tych ośrodków n1 i n2.
17. Soczewki
Program pozwala prześledzić geometryczną metodę wyznaczania obrazu wytwarzanego przez soczewkę skupiającą i rozpraszającą. Przedmiot jest przedstawiony schematycznie w postaci strzałki prostopadłej do głównej osi optycznej, a w celu wyznaczenia jego obrazu znajdujemy położenie obrazu wierzchołka strzałki, wykreślając dwa promienie: promień przechodzący przez środek soczewki, który nie zmienia swego kierunku, oraz promień padający równolegle do osi optycznej, który po przejściu przez soczewkę skupiającą biegnie przez ognisko, a po przejściu przez soczewkę rozpraszającą biegnie tak, że jego przedłużenie przechodzi przez ognisko pozorne. W programie można zmieniać położenie przedmiotu i soczewki. Można również zmieniać ogniskową soczewki, zmieniając jej promień krzywizny. W programie dostępna jest też opcja powiększania i pomniejszania obrazu.
18. Interferencja na pojedynczej szczelinie
Interferencja światła była pierwszym eksperymentem wskazującym na jego falowy charakter. Program pozwala obserwować wynik interferencji dwóch spójnych fal świetlnych powstałych w wyniku przejścia płaskiej fali świetlnej przez przesłonę z dwoma punktowymi szczelinami (doświadczenie Younga). W programie można za pomocą odpowiednich suwaków zmieniać odległość między szczelinami \(d\), odległość szczelin od ekranu \(L\) oraz długość fali \(\lambda\) i obserwować, jak obraz interferencyjny zależy od tych parametrów. Na wykresie przedstawiony jest również rozkład natężenia światła (fali).
19. Dyfrakcja na pojedynczej szczelinie
Dyfrakcja światła jest zjawiskiem wskazującym na jego falowy charakter. Program pozwala obserwować wynik dyfrakcji fal świetlnych powstałych w wyniku. przejścia płaskiej fali świetlnej przez przesłonę z jedną szczeliną. Zjawisko dyfrakcji polega na uginaniu się światła przechodzącego w pobliżu przeszkody. W opisywanym doświadczeniu to ugięcie następuje na brzegach szczeliny. Natężenie światła w dowolnym punkcie na ekranie umieszczonym za szczeliną jest wynikiem nakładania się wszystkich zaburzeń falowych docierających do ekranu z różnych punktów szczeliny. W programie można zmieniać szerokość szczeliny \(a\), odległość szczeliny od ekranu \(L\) oraz długość fali \(\lambda\) i obserwować, jak obraz dyfrakcyjny zależy od tych parametrów.
20. Dyfrakcja na dwóch szczelinach
Program pozwala obserwować wynik równoczesnej dyfrakcji i interferencji fal świetlnych powstałych w wyniku przejścia płaskiej fali świetlnej przez przesłonę z dwoma szczelinami. Dla szczelin o skończonej szerokości (nie punktowych) w wyniku interferencji fał otrzymujemy obraz, w którym natężenia prążków nie są stałe (jak w doświadczeniu Younga), ale zależne od obrazu dyfrakcyjnego pojedynczej szczeliny. Mamy do czynienia z następującą sytuacją: w pewnym punkcie ekranu natężenie światła, z każdej szczeliny osobno, jest dane przez obraz dyfrakcyjny tej szczeliny, obrazy dyfrakcyjne dwóch szczelin rozpatrywanych oddzielnie nakładają się (fale interferują). Otrzymany obraz jest więc iloczynem czynnika interferencyjnego i dyfrakcyjnego. W programie można zmieniać szerokość szczelin \(a\), ich wzajemną odległość \(d\), odległość szczelin od ekranu \(L\) oraz długość fali \(\lambda\), i obserwować, jak obraz dyfrakcyjny zależy od tych parametrów.
-
-
-
21. Ciało doskonale czarne
Program pozwala śledzić zależność widmowej zdolności emisyjnej ciała doskonale czarnego od temperatury. Wartość temperatury można zmieniać w zadanym zakresie i w zadanych przedziałach temperatur. W programie można zapisać wykres (dla danej temperatury) celem porównania go z rozkładem dla innej temperatury.
22. Rozpad promieniotwórczy
Rozpady promieniotwórcze dostarczają wielu informacji zarówno o jądrach atomowych, ich budowie, stanach energetycznych, oddziaływaniach, jak również wielu zasadniczych informacji o pochodzeniu wszechświata. Program ilustruje prawo promieniotwórczego rozpadu nuklidów. W procesie rozpadu nuklid promieniotwórczy spontanicznie emituje pewną cząstkę i ulega przemianie w inny nuklid (dolny rysunek w programie). Liczba nuklidów pierwiastka ulegającego rozpadowi maleje z biegiem czasu, tak jak przedstawiono w programie na górnym wykresie. Rozpadu nuklidów opisuje się za pomocą tzw. czasu połowicznego zaniku (rozpadu) \(T_{1/2}\), który informuje, po jakim czasie liczba jąder promieniotwórczych zmaleje o połowę. Ten parametr można zmieniać w programie.
23. Zjawisko fotoelektryczne
Program pozwala na poznanie podstawowych własności zjawiska fotoelektrycznego zewnętrznego wykorzystując do tego układ pomiarowy z fotokomórką. W programie można zmieniać natężenie światła, jego częstotliwość (w zakresie widzialnym i nadfiolecie) oraz napięcie U przyłożone między elektrody fotokomórki.
24. Funkcje falowe elektronu
Funkcje falowe elektronu (będące rozwiązaniem równania Schrödingera) zależą od trzech liczb kwantowych n, l, m. Fizyczną interpretację funkcji falowej zaproponował Max Born. Zgodnie z nią kwadrat modułu funkcji falowej wyraża prawdopodobieństwo znalezienia cząstki w danym obszarze (jest miarą gęstości prawdopodobieństwa). Program wykreśla, dla wybranych liczb kwantowych (n, l, m), radialne funkcje falowe atomu wodoru, radialną i kątową gęstość prawdopodobieństwa oraz wizualizację orbitali atomu wodoru w 2 wymiarach.
-
